Uma mola é comprimida em e possui constante elástica igual a , após ela ser liberada, ela empurra uma bola de massa . Qual será a velocidade obtida pela bola caso seja lançada na horizontal e qual será a altura obtida caso seja lançada na vertical para cima?
Considere a aceleração da gravidade igual a .
Passo 1
Bom pessoal, temos duas situações nesse enunciado, vamos desenhar cada uma
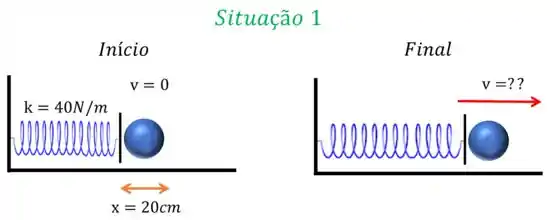
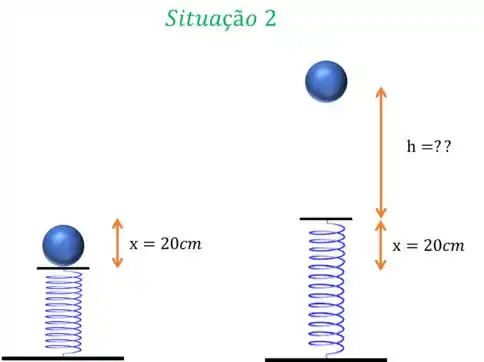
vamos pensar em uma coisa, quando a mola está sendo comprimida, ela tem uma energia potencial elástica armazenada, correto? Então vamos calcular essa energia
Em que é a constante elástica da mola é a deformação em metros!
Passo 2
Vamos nos concentrar na situação primeiro
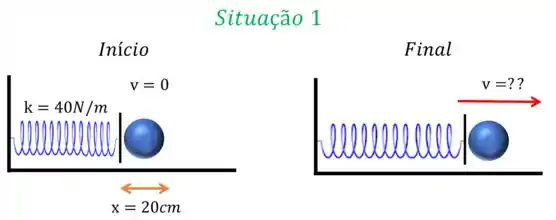
Vamos lembrar quais são os dados do enunciado, a mola tem a constante elástica igual a:
E uma compressão igual a:
Sabemos que a deformação deve ser dada em metros, logo temos que fazer essa transformação apenas dividindo por :
Substituindo esses valores na fórmula da energia potencial elástica:
Teremos então:
Elevando ao quadrado:
Vamos fazer essa multiplicação no numerador:
Resumimos a uma última divisão igual a:
Beleza, encontramos a energia armazenada inicialmente em forma de energia potencial elástica!
Passo 3
Como a mola está comprimida, quando soltar o sistema, ela será empurrada pela mola e ganhará uma velocidade. Ou seja, a energia potencial elástica está se transformando em energia cinética! E a energia cinética pode ser calculada como
Já conhecemos a massa da bola:
E já sabemos que se a energia cinética é igual a energia potencial elástica:
Lembra que já calculamos essa energia potencial elástica? Vou refrescar sua memória
Então
E podemos usar a fórmula da energia cinética aqui
Passo 4
Sabemos também o valor da massa que foi dada no enunciado
Mas precisamos passar essa massa para quilogramas. Para fazer isso, vamos dividir por
Substituindo o valor da massa:
Simplificando o por
Passando o para o outro lado dividindo
Após a divisão, encontramos o valor da velocidade ao quadrado:
Como na realidade nós queremos a velocidade, precisamos tirar a raiz quadrada dos dois lados da igualdade:
Essa raiz será igual a:
Logo, a bola lançada na horizontal atinge uma velocidade igual a .
Passo 5
Agora vamos olhar para a situação
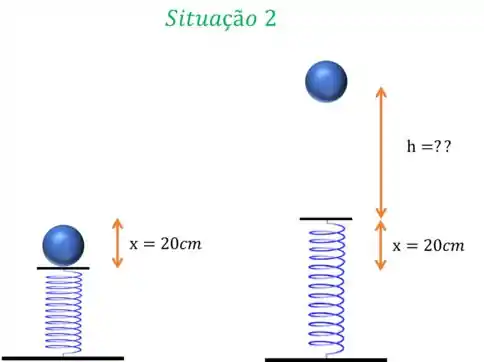
Se lançarmos essa bola para cima, concorda comigo que ela vai subir até uma altura máxima no ar? Então ela ganhará uma energia potencial gravitacional! E qual é a fórmula da energia potencial gravitacional? Ah lembrei:
Além da massa e da aceleração da gravidade , nós também precisamos da altura que a bola chega .
Passo 6
Nós temos acesso a massa igual a:
e já fizemos a conversão da unidade para quilograma lá no passo
Conhecemos a aceleração da gravidade é igual a:
E desejamos saber a altura . Logo, a energia potencial gravitacional dada pela fórmula:
É igual a:
Agora pensem comigo. Na situação inicial a bola está em repouso e a mola começa a empurrar, mas a velocidade inicial é zero! Então no início não teremos energia cinética
E no final, quando a bola atinge a altura máxima, a velocidade também tem que ser zero (se fosse diferente de zero ela subiria mais um pouco, não é mesmo?). Então a energia cinética final também será zero
Ou seja... não precisamos nos preocupar com a energia cinética 😊
Como a energia potencial elástica da mola se transformou em energia potencial gravitacional, podemos igualar essas duas energias:
E lembram quanto que encontramos para a energia potencial elástica?
Vamos igualar as duas energias agora para fazer a conservação
Passo 7
Podemos calcular a altura , se a isolarmos de um lado só da igualdade:
Multiplicando por , temos:
Fazendo a divisão
Ou seja, a altura que a bola atinge se lançada na vertical é igual a metros!
Resposta
e