Um passeio de montanha-russa num parque de diversões parte do repouso a uma altura de acima do solo e rapidamente inicia a descida pelo trilho. Num certo momento, a pista faz um loop e o trem atinge uma outra altura de . Qual a velocidade do trem nesse momento, considerando que a carga completa do trem mais as pessoas sobre ele tem uma massa de ?
Considere .
Passo 1
Vamos imaginar essa cena? Eu acho que fica mais fácil!
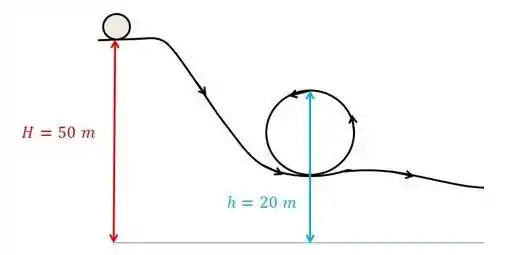
A gente sabe que quando fala que o carrinho está inicialmente em repouso, a velocidade inicial é igual a zero:
Desejamos saber a velocidade final, quando ele estive na parte mais alta do loop
Porém os outros dados fornecidos pelo enunciado são:
Passo 2
Como a velocidade inicial é igual a zero, a energia cinética inicial é:
Substituindo os valores iniciais:
Logo a energia cinética inicial é igual a zero!
Passo 3
Mas e quanto a energica potencial gravitacional diretamente ligada a altura inicial do objeto? Bom, a energia potencial gravitacional é dada pela equação:
Substituindo os valores iniciais:
Que quando multiplica tudo
Encontramos o valor da energia potencial gravitacional!
OBS: Podemos usar a energia potencial tanto com a letra quanto com , cada livro escreve de uma forma e cada professor escolhe a que acha melhor. Aqui usaremos sempre a notação com , ok? 😊
Passo 4
Quando o trem atinge a altura do loop igual a , a energia potencial gravitacional final é igual a:
Que quando multiplica tudo
Perceba que a energia potencial gravitacional final é menor do que a inicial. Para onde será que foi essa diferença de energia?
Foi convertida em energia cinética, pois o carrinho ganhou velocidade!
Passo 5
Nós não sabemos a velocidade final, mas vamos calcular a energia cinética final e ver quais são os dados que temos que calcular:
Substituindo a massa que já conhecemos:
A única coisa que dá para fazer nessa energia cinética é a simplificação do pelo
Passo 6
Vamos conservar a energia? Então vamos igualar a energia mecânica inicial e final:
Substituindo os valores que encontramos:
Vemos que a única variável da equação é a velocidade final que queremos encontrar, então vamos passar todos os números para o outro lado:
Resolvendo essa subtração temos:
Vamos passar o que está multiplicando para o outro lado dividindo
Fazendo essa divisão
Precisamos então tirar a raiz quadrada dos dois lados da conta:
Que resulta em uma velocidade final igual a:
Não esquece a unidade, porque já chegamos na nossa resposta final!
Resposta
b)