(Adaptada) Uma bomba Peerless horizontal de carcaça bipartida do tipo , com diâmetro de rotor e operando com leva água de um reservatório a outro por tubos de ferro fundido com de e de de montados em série. A diferença de altura entre os reservatórios é de . Esboce um gráfico da curva de operação do sistema.
Dados: A viscosidade cinemática do fluido é dada por e a rugosidade do ferro fundido é .
Passo 1
Vamos primeiro organizar nossos dados! O sistema possui dois trechos de tubulação de ferro fundido com de comprimento, tendo um deles () de diâmetro e o segundo, (). Além disso, a diferença de altura entre os reservatórios é de .
A curva do sistema nada mais é do que um gráfico de carga do sistema () por vazão volumétrica (). Então, nosso trabalho aqui é calcular com um conjunto de valores para . Então, bora lá! ^^
Seja o sistema ilustrado abaixo (não muito artístico, mas com carinho ahaha):
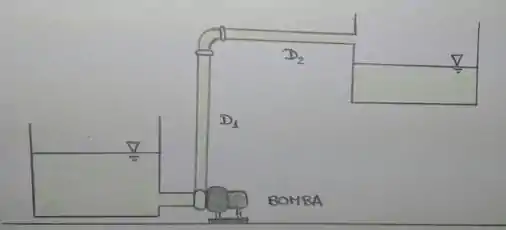
Aplicando o balanço de energia entre os dois reservatórios, temos que:
Assumindo que os dois reservatórios são abertos, temos que: . Além disso, a velocidade com que a altura do líquido no reservatório varia é muito pequena, então desprezamos as velocidades e .
Com essas considerações:
Já conhecemos e é a aceleração da gravidade. Precisamos agora encontrar a perda de carga do sistema .
Passo 2
Vamos desprezar os possíveis acidentes do sistema por não terem sido mencionados e calcular somente as perdas de carga das duas tubulações em série.
A gente já viu que a perda de carga em uma tubulação pode ser calculada por:
Em que é o fator de atrito obtido pelo diagrama de Moody ou via equação de Colebrook ou ainda pela equação (explícita) de Milliard.
Dessa maneira, ficamos com:
Podemos expressar a velocidade por meio da vazão volumétrica da seguinte forma:
Assim:
A rugosidade relativa é dada por:
Além disso, para o Segundo tubo:
Assim:
A rugosidade relativa é dada por:
Logo:
Substituindo as velocidades em função da vazão, teremos:
Agora, temos uma expressão geral para a carga do sistema. Basta escolhermos alguns valores de vazão e calcularmos os fatores de atrito correspondentes (pelo diagrama de Moody, ou pela equação de Colebrook ou pela equação de Milliard) e qual a carga !
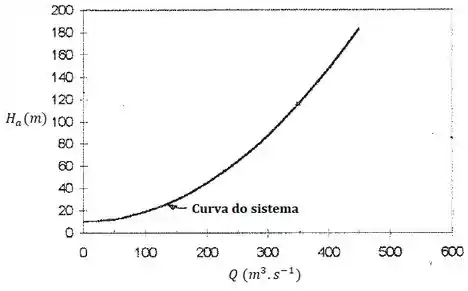
Fazendo isso para alguns pontos, teremos um comportamento gráfico parecido com esse:
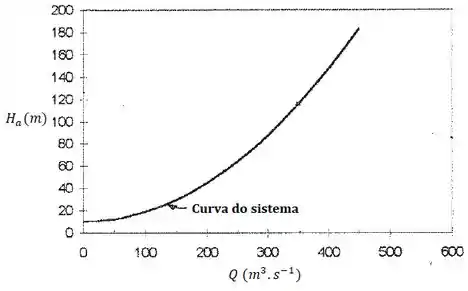
Resposta