(Adaptada) Uma bomba Peerless horizontal de carcaça bipartida do tipo 4AE12, com diâmetro de rotor 11 in., e operando a 1750 rpm, leva água de um reservatório para outro; eles são conectados por 200 ft de tubo de 4 in., seguidos de 200 ft de tubo de 3 in. em série (os tubos são de ferro forjado). A diferença de altura entre os reservatórios é de 10 ft. Despreze as perdas localizadas. Calcule a carga do sistema para uma vazão Q = 0,001 m³/s.
Passo 1
Novamente temos um problema em que uma bomba auxilia o escoamento de um fluido de um reservatório para o outro. Esse exercício pede para encontrarmos a carga do sistema para uma determinada vazão.
Para isso, vamos utilizar a definição de pela equação da energia
O volume de controle escolhido engloba os dois reservatórios passando pelas duas tubulações e pela bomba.
Com essa escolha, assumimos que
pois as superfícies estão submetidas à pressão atmosférica e nelas a área é tão grande que a velocidade é aproximadamente zero.
Sobre as elevações o enunciado diz que
Atualizando a equação do
Passo 2
Para calcular essa perda de carga, vamos lembrar por onde esse fluido está passando. São 2 tubulações de ferro forjado em série: uma de 4 polegadas de diâmetro e 200 ft de comprimento e outra com o mesmo comprimento, mas com diâmetro de 3 polegadas.
Passando para o Sistema Internacional
Para calcular as velocidades, vamos usar a vazão volumétrica
Na tubulação A
Na tubulação B
Para encontrar a perda de carga está faltando saber quem é o fator de atrito. Vamos resgatar o que aprendemos no assunto Escoamento Interno Viscoso e Incompressível.
Dica: Se quiser, dê uma olhadinha lá depois para dar aquela revisada, mas fica tranquilo que vou explicar um pouquinho aqui também!
Passo 3
Para sabermos se vamos calcular o fator de atrito por ou pelo Diagrama de Moody, precisamos saber se o escoamento é laminar ou turbulento. Isso é uma tarefa para o senhor Reynolds!
Na tubulação A
Logo, vamos calcular pelo Diagrama de Moody pois é um escoamento turbulento
Na tubulação B
Diagrama de Moody para a parte B também!
Além do Reynolds, precisamos da rugosidade relativa para calcular o fator de atrito por Moody. A rugosidade do ferro forjado é aproximadamente 0,05 mm
O cálculo da rugosidade relativa é
Com os pares rugosidade relativa e Reynolds, usamos o Diagrama de Moody
De verde, os dados da tubulação A. Em azul, a tubulação B.
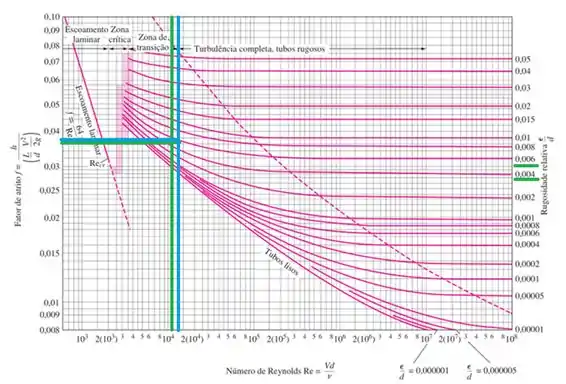
Do lado esquerdo do Diagrama de Moody, se faz a leitura dos fatores de atrito
E assim, finalmente, podemos calcular a perda de carga
Substituindo os valores encontrados
Passo 4
Finalmente, vamos calcular a carga do sistema pedida no enunciado :D
Resposta
A carga do sistema para Q = 0,001 m³/s é