(Adaptada) Queremos usar a bomba de da figura abaixo a para bombear água a de um reservatório para outro a de altura de de tubo com diâmetro interno de com um fator de atrito . Assuma que ambos reservatórios são abertos para a atmosfera e que a curva da bomba de segue o seguinte comportamento:
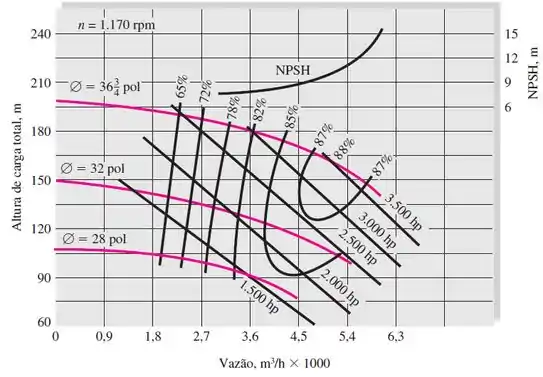
- Qual será o ponto de operação?
- Qual o rendimento no ponto de operação?
Passo 1
Nosso primeiro passo será avaliar com a altura da carga do sistema em questão! A gente sabe que o sistema é composto por dois reservatórios, distando verticalmente um do outro e eles são conectados por de tubo (diâmetro de e .
Pela equação de Bernoulli aplicada ao sistema, temos que:
Como a velocidade do fluido nos reservatórios é desprezível e ambos estão a mesma pressão () por estarem abertos, a altura de carga do sistema é dada por:
A perda de carga na tubulação é dada por:
Podemos reescrever a expressão em termos da vazão volumétrica e assim:
Substituindo na expressão:
Logo:
Passo 2
Antes de substituir todos os dados, vamos converter o diâmetro em unidades S.I.:
Substituindo os valores informados pelo enunciado:
Como a figura utiliza a vazão volumétrica em , podemos reescrever a equação para:
Passo 3
Agora, a gente pode traçar a curva do sistema e ver em que ponto ela intercepta a curva de altura de carga da bomba com de diâmetro. Comparando as duas curvas ��no olho”, a gente tem:
Mas, para encontrar o valor analiticamente, vamos utilizar a curva fornecida pelo enunciado para a bomba de :
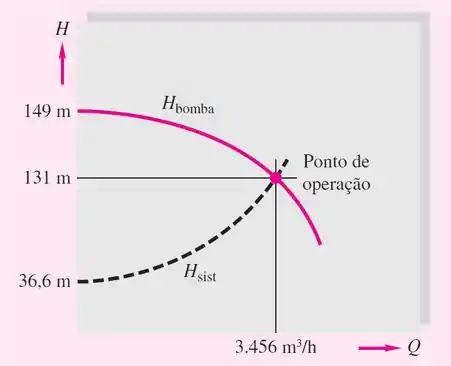
O ponto de operação se refere ao ponto em que as curvas se cruzam, então, para encontra-lo a gente pode fazer o seguinte:
Com essa vazão, a altura de carga da bomba equivale a:
Note que o valor foi equivalente ao que achamos “no olho”! ^^
Passo 4
Pelo gráfico, podemos ver que esse ponto está próximo da curva de rendimento de :
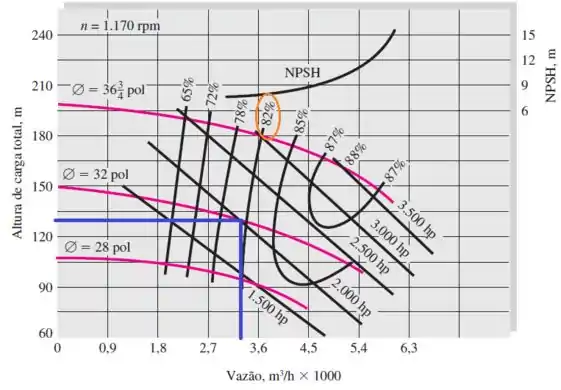
Logo, o rendimento nesse ponto pode ser admitido como aproximadamente:
Resposta
- O ponto de operação é aquele em que:
- O rendimento nesse ponto equivale a: