Uma bomba centrífuga de de diâmetro de rotor girando a com água a gera os seguintes dados:

Trace curvas de desempenho desta bomba; inclua uma curva de eficiência versus a vazão volumétrica. Localize o ponto de melhor eficiência e especifique a capacidade da bomba neste ponto.
Passo 1
Para construirmos a curva da bomba, temos que plotar os dados de carga () versus vazão volumétrica (). Beleza! Isso foi informado pra gente já na tabela!
Além disso, foi pedida a curva de eficiência () e, então, a gente precisa calcular esses valores para cada ponto. Sabemos que a eficiência é definida como:
Pela tabela, a gente consegue diretamente os valores da potência do motor (), que é denominada
Precisamos agora calcular a potência da bomba () e a gente sabe que ela é dada por:
Ou seja, para cada conjunto de valores de vazão volumétrica () e perda de carga (), teremos uma potência da bomba diferente.
Dessa maneira, a gente conseguirá calcular a eficiência por meio da equação:
Ao organizar todos os valores numa tabela, temos que:
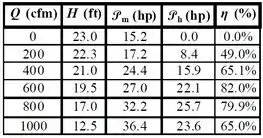
Agora é só plotar o gráfico com os valores de abscissa sendo a vazão volumétrica () e duas curvas: uma com a carga () – curva em vermelho - e outra com a eficiência () – curva em azul:
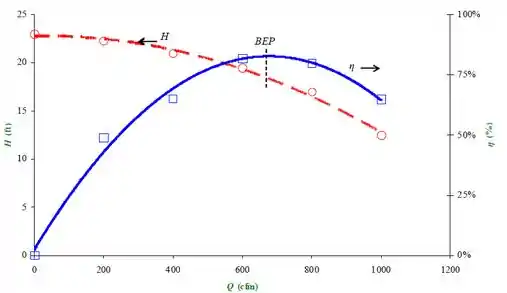
Essas curvas são interpolações de segundo grau dos dados que temos, ou seja, são parábolas que melhor se aproximam dos nossos dados. Podemos fazer isso no Excel, por exemplo. Como resultado, obtivemos:
O ponto de melhor desempenho é aquele cuja eficiência é máxima. Então, para encontrar o ponto máximo, basta verificar o valor de que anula a derivada da função:
Agora, se a gente jogar esse valor na equação da eficiência, teremos que:
Para descobrir o respectivo valor da carga, a gente pode jogar a vazão encontrada na equação da carga e assim:
Resposta
As curvas são da seguinte forma:
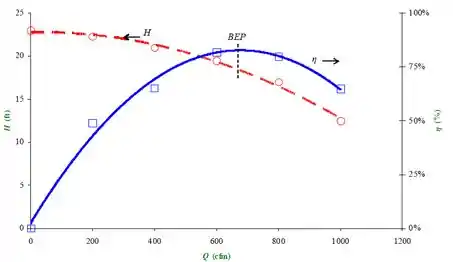
No ponto de máximo desempenho, temos que: