Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Degrau e Tunelamento

Ver Teoria
Exercício 5123467

Enunciado

USP, Física 4, P3 2017, 1

Uma partícula de massa m que se move em uma dimensão possui energia potencial que

varia com a posição como mostra a figura.

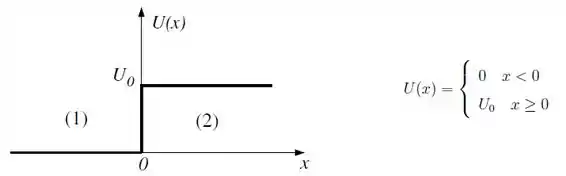
A partícula está em um estado estacionário com energia E φ 1 x   e

φ 2 x da equação de Schrödinger correspondente aos intervalos x ≥ 0

(região 2) respectivamente, são

φ 1 x = A . e i k x + B . e - i k x

φ 2 x = C . e - K x + D . e K x

onde A, B, C e D são constantes arbitrárias.

(a) Determine D. justifique.

(b) Calcule k e K em função de m, E, U0 e ћ.

(c) Para A = 1, determine B e C.

Passo 1

No primeiro item da questão, devemos nos atentar ao fato de que se trata de uma questão sobre degrau de tunelamento.

Logo sabemos que aprece uma barreira potencial no caminho da nossa partícula. Como a questão pede o valor de D, precisamos ver que quando a partícula se encontra na região 2 ela deve respeitar o fato de que para x ≥ 0 temos que U x = U 0 .

Analisando a nossa equação temos que

φ 2 x = C . e - K x + D . e K x

Mas perceba que se fizermos x - > ∞ a nossa equação também tenderá ao infinito devido ao termo.

D . e K x

Logo a única maneira de limitarmos a equação de onda φ 2 x é com o valor de D = 0 .

Passo 2

Para o item b) temos que lembrar das fórmulas principais da física quântica.

A fórmula geral de Schrödinger é dada por

- ћ 2 2 m d 2 φ x d x 2 + U x . φ x = E φ x

Sabemos que em casos de degraus de tunelamento podemos escrever a fórmula de Schrödinger de forma simplificada para a região 1 reescrevendo ela como

d 2 φ 1 x d x 2 = - 2 m E ћ 2 φ 1 x

Isso acontece pois sabemos que na Região 1 o valor de U0=0, logo totó o termo U x . φ x ira sair da conta, depois apenas isolamos a derivada.

Mas sabemos que φ 1 x = A . e i k x + B . e - i k x

Substituindo isso na nossa equação teremos que

d 2 φ 1 x d x 2 = - A . k 2 e i k x - B . k 2 . e - i k x = - k 2 ( φ 1 x )

Igualando ambos os lados das equações encontradas teremos que

d 2 φ 1 x d x 2 = - 2 m E ћ 2 φ 1 x = - k 2 ( φ 1 x )

Logo teremos que

k 2 = 2 m E ћ 2

k = 2 m E ћ

Passo 3

Para a região 2 podemos escrever a equação de Schrödinger também de forma simplificada.

- ћ 2 2 m d 2 φ x d x 2 + U x . φ x = E φ x

Nesse caso sabemos que na região 2 , U x = U 0 , substituindo na equação e isolando a derivada teremos que

d 2 φ 2 x d x 2 = 2 m ( U 0 - E ) ћ 2 φ 2 x

Sabemos também que para região 2 a equação de onda é dada por

φ 2 x = C . e - K x + D . e K x

Em que já sabemos que também podemos simplifica-la para equação

φ 2 x = C . e - K x

Teremos então que a derivada nesse caso será dada por

d 2 φ 2 x d x 2 = C . K 2 . e - K x = K 2 φ 2 x

Igualando os dois valores que encontramos para derivada teremos que

K 2 = 2 m ( U 0 - E ) ћ 2

Logo

K = 2 m ( U 0 - E ) ћ

Passo 4

Agora para o ultimo item é pedido que definamos os valores de B e C sabendo que A=1.

Para isso vamos nos aproveitar da continuidade das funções no ponto em que X=0, sabemos que para esse ponto as equações de ondas são iguais, ou seja, podemos dizer que   φ 1 0 = φ 2 0 . Além disso também podemos fazer a mesma afirmação quanto as suas derivadas, ou seja   φ 1 ' 0 = φ 2 ' 0

Fazendo os cálculos para φ 1 0 = φ 2 0 teremos que

φ 1 0 = A . e i k 0 + B . e - i k 0

φ 1 0 = 1.1 + B . 1

φ 1 0 = 1 + B

φ 2 0 = C . e - K 0 + 0 . e K 0

φ 2 0 = C

Igualando os termos teremos a primeira equação do nosso sistema

1 + B = C

Sabemos que também podemos fazer a mesma relação no que se refere as derivadas

Fazendo os cálculos para φ 1 ' 0 = φ 2 ' 0 teremos que

φ 1 ' 0 = A . i k . e i k 0 - B . i k . e - i k 0

φ 1 ' 0 = 1 . i k - B . i k

φ 2 ' ( 0 ) = C . - K e - K 0 + 0 . K . e K 0

φ 2 ' ( 0 ) = - K C

Igualando os termos teremos a segunda equação do nosso sistema

1 . i k - B . i k = - K C

Logo o nosso sistema de equações será dado por

1 + B = C i k - B i k = - K ( 1 + B )

Resolvendo o sistema teremos

i k + K = - K B + B i k

B = i k + K i k - K

E substituindo na primeira equação teremos

1 + i k + K i k - K = C

Logo

C = 2 i k i k - K

Resposta

a) D = 0

B) k = 2 m E ћ ; K = 2 m ( U 0 - E ) ћ ;

C) B = i k + K i k - K

C = 2 i k i k - K ;

Exercícios de Livros Relacionados

72 . Em um arranjo como o das Figs. 38 - 14 e 38 - 15 , os elétrons do feixe incidente têm uma velocidade de 1,60 × 10 7 m s e na região 2 existe um potencial elétrico de V 2 = - 500V . Qual é o númer
73 . A corrente de um feixe de elétrons, todos com uma velocidade de 900m / s , é 5,00m A . Se o feixe incide em um degrau de potencial com uma altura de - 1,25μ V , quanto é a corrente do outro lado
Uma partícula de energia E se aproxima de uma barreira de degrau da altura U0. Qual deve ser a razão E / U0 para que o coeficiente de reflexão seja 1/2?