Derive a função
Passo 1
Fala, galera! Com é que vocês estão? Muita ralação? Então agora pode relaxar, porque aqui vai ser tudo explicado passo a passo com muita calma!
Essa função pode te assustar um pouco por causa da variável . Estamos muito acostumados a fazer exercícios com . Mas se a gente substituísse esse por , o susto passaria?
Quando a gente substituiu por , a gente apenas mudou o nome da variável. Isso não muda em nada o passo a passo que vamos seguir para derivar a função! Isso quer dizer que o nome da variável não importa! Podemos derivar a função com , imaginando que estamos derivando uma função com , beleza? Então, vamos voltar para a função do enunciado!
Essa questão parece ser difícil, porque a função está escrita de uma maneira complicada. No entanto, nós podemos reescrever essa função de uma forma mais simples. Tá vendo esse na frente do parêntese? Ele está aí multiplicando todo mundo que está dentro dos parênteses. Vamos aplicar a multiplicação distributiva, “distribuindo” mesmo ele em todos os termos que estão lá dentro dos parênteses.
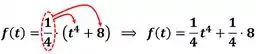
Agora temos uma multiplicação da fração por valores inteiros: e . Quando isso acontece a gente multiplica só a parte de cima e repete a pare de baixo:
A fração
Logo:
Essa nova função assusta menos, não é mesmo?
Agora que simplificamos a função, podemos começar a derivar.
Passo 2
Para derivar uma função com somas a gente lembrar que termos somados ou subtraídos podem ser olhados separadamente, assim a nossa vida vai ficar muito mais fácil! Levando isso em conta, a derivada de pode ser reescrita como está abaixo.
Sempre que a gente precisar derivar uma função grande cheia de somas e subtrações, podemos derivar cada termo de forma separada e depois juntar tudo para calcular a derivada da função inteira! Vamos calcular a derivada de cada termo separadamente no próximo passo!
Passo 3
Para calcular a derivada de , usaremos a regra do peteleco! Nessa regra, a derivada faz o expoente “cair” e passar a multiplicar o termo. Além disso, o expoente da derivada vira o expoente antigo menos .
No termo , o expoente vai “cair” e passar a multiplicar. O novo expoente será .
Como estamos multiplicando e dividindo por 4, as operações se cancelam e podemos cortar o em cima e embaixo.
Agora, vamos calcular a derivada da constante . Para isso, temos que lembra que derivar é a mesma coisa que calcular a taxa de variação! Se o termo não varia, como é o caso de uma constante, então sua taxa de variação vale zero!
Ou seja, como não varia em relação a , sua derivada vale .
Já que temos os valores de cada derivada, podemos juntar todos eles para calcular a derivada total da função .
Passo 4
Agora podemos substituir todos esses valores de derivadas na equação da derivada da função (segunda equação do passo 2).
Boaaa! Esse é o fim de mais um exercício de derivadas! Estamos voando!