Encontre a primeira e segunda derivada da função
Passo 1
Fala aí! Tudo joia?
Essas raízes ai podem até confundir um pouco a nossa mente no começo, mas pra gente derivar essa função, vamos usar a “Regra do Tombo”. Em cada termo daquele, o expoente vai “cair” pra frente multiplicando e vai perder uma unidade. Desse jeito aqui:
E você dever estar se perguntando: mas que expoente, gente? Bem, quando temos uma raíz, podemos reescrevê-la em forma de potência, e esse será o nosso primeiro passo.
Passo 2
Para reescrever as raízes em forma de potências, precisamos usar essa regra aqui:
Nossa raíz será transformada em uma potência onde o expoente é uma fração. No numerado (parte de cima da fração) vai ficar o valor que o estiver elevado antes quando ainda estava dentro da raíz, e no numerador (parte de baixo da fração) vai ficar o índice da raíz.
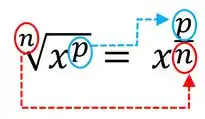
Então no nosso caso, em não aparece valor nenhum, isso porque é uma raíz quadrada, então o índice da raíz e o . Além disso, o não está elevado a número nenhum, e pra ajudar a gente, vamos colocar o 1 no expoente dele. Vai ficar assim:
E para o
Nossa função então pode ser escrita como:
Passo 3
Agora vamos partir pra usar a Regra do Tombo! Montando vai ficar assim:
Vamos dar um pause aqui na derivada e vamos resolver essa subtração entre frações, que está nos exponentes, no próximo passo...
Passo 4
A gente tem que resolver:
A gente só pode somar ou subtrair frações se elas tiverem os denominadores iguais, lembra?
Nesse caso aqui a gente pode fazer um esqueminha bem legal que é reescrever o como uma fração com o denominador que a gente precisa. Pra isso a gente vai dizer que nosso pode ser escrito com:
Agora que ele tem o denominador . Nossa continha fica:
Agora que os denominadores ficaram iguais, a gente resolve em cima, e embaixo a gente repete:
Na outra é a mesma coisa:
Agora já conhecemos os valores dos expoentes da nossa derivada.
Passo 5
Vamos voltar isso pra derivada agora:
Outro detalhe importante. Como os expoentes estão negativos, a gente vai jogar as potências pro denominador:
E agora a gente pode voltar pra forma de raiz:
Prontinho! Essa é a primeira derivada😉
Passo 6
Vamos pra segunda derivada agora. É da mesma forma, só que a gente vai derivar a função , beleza?
Pra facilitar um pouquinho, vamos pegar nessa forma aqui:
Show! Agora vamos aplicar a Regra do Tombo nela:
Passo 7
Essas continhas aí a gente vai resolver da mesma maneria que fizemos ali atrás! Vai ficar assim:
Vamos jogar o que tá com expoente negativo pra baixo:
E vamos colocar na forma de raiz:
E pronto! Essa é a segunda derivada 🤓