Encontre uma equação para a reta tangente à curva no ponto dado.
Passo 1
Fala aí, tudo joia?
Olha só, sempre que falar de equação de reta tangente, a gente vai usar derivada!
Isso porque uma reta tem essa forma aqui:
Onde é a inclinação (coeficiente angular) da reta e é um ponto da reta.
E esse é justamente a o valor da derivada da função no ponto . Sacou?
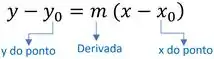
Bora ver isso na prática!
Passo 2
Como a gente precisa da derivada, vamos começar derivando a função:
A gente deriva com a regra do Tombo, que é assim:
Vamos derrubar esses expoentes então!
Beleza! Já derivamos a função!
Passo 3
Agora a gente precisa do valor dessa derivada no ponto que nos deram, no caso:
O ponto tem sempre uma ordem específica, primeiro o valor do e depois do valor do .
Então o ponto tem e .
Substituindo na nossa derivada o , a gente tem:
Esse aí é o coeficiente angular da reta, o nosso !
Passo 4
Voltando pra equação da reta tangente agora:
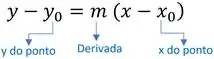
A gente já tem e temos o ponto . Só jogar ali agora e correr pro abraço!
O que podemos também fazer aqui é dar uma pequena arrumada. Vamos multiplicar esse 3 através da distributiva:
Agora vamos deixar o sozinho jogando o para o outro lado somando:
Prontinho! Essa é a equação da reta tangente no ponto pedido😉
Resposta
.