Seja a transformação , e seja um paralelepípedo. O volume do paralelepípedo transformado T(Q), em relação ao volume de Q:
(a) É o mesmo.
(b) É maior.
(c) É menor.
(d) Pode ser maior ou menor, dependendo de Q.
Passo 1
Pra resolver a questão vamos usar o seguinte teorema:
Se a gente tem uma transformação linear e um conjunto qualquer de , então o volume de é igual ao volume de vezes , onde A é a matriz que representa a transformação T.
Vamos trabalhar com a base canônica do pra facilitar.
Passo 2
O enunciado nos deu que:
Para acharmos a matriz A que representa essa TL na base canônica, basta a gente “decompor” essa expressão dessa forma:
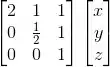
Repara que na primeira coluna temos os coeficientes do x, na segunda os coeficientes do y e na terceira os coeficientes do z.
A matriz que A é a matriz do lado esquerdo dessa expressão, então agora é só achar o determinante dela.
Só que A é uma matriz diagonal superior, logo seu determinante é igual ao produto dos elementos da diagonal principal, ou seja:
Usando o resultado do teorema que vimos no passo 1:
Então o volume dos dois é o mesmo.
Resposta
(a) É o mesmo.