UFRJ, Física 4, P1 2017.2, 8
Em uma palestra, um professor aponta um “laserpointer” de cor vermelha () para o quadro. Observa-se que o raio da mancha do feixe de luz no quadro é de . Qual o raio do diafragma do laser-pointer, por onde sai o feixe de luz, se a distância entre a caneta e o centro da mancha de luz no quadro é de 9,0m?
(a)
(b)
(c)
(d)
(e)
(f)
Passo 1
Antes de qualquer coisa devemos nos lembrar que esse caso se trata de um caso de difração por fenda circular, ou seja, precisamos relembrar qual a fórmula para o caso em que temos uma difração desse tipo.
Nesse caso a fórmula é
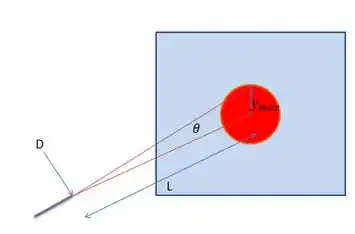
Visualmente a nossa fórmula simboliza os seguintes dados
Agora você tem que lembrar o seguinte, para ângulos muito pequenos podemos falar que
E pelo nosso desenho temos que
Passo 2
Substituindo na nossa equação teremos
Nesse caso é o Raio da nossa imagem e D é o diâmetro do furo pelo qual temos difração, como o nosso objetivo é determinar exatamente o valor do diâmetro do furo, vamos isolar o valor de D e teremos a seguinte fórmula.
Passo 3
Nossos dados são
Substituindo teremos
Como queremos o raio
Resposta
(c) 1, 2mm