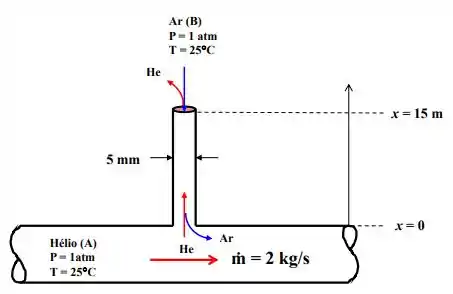
A pressão em uma tubulação que transporta gás hélio a uma taxa de é mantida a pela ventilação de hélio para a atmosfera através de um tubo de de diâmetro interno, que se estende no ar, como mostrado na Figura. Supondo que ambos, o hélio e o ar atmosférico, estão a , determinar:
- a vazão mássica de hélio perdido para a atmosfera através do tubo;
- a vazão e a fração mássica de ar que se infiltra na tubulação;
- a velocidade do escoamento no fundo do tubo onde este está ligado à tubulação que vai ser medida por um anemômetro em regime permanente.
Dados: O coeficiente de difusão do hélio no ar .
A Massa molar do ar e a do hélio
A constante dos gases
Passo 1
Fala aí! Vamos começar fazendo algumas suposições que nos ajudem a resolver nosso exercício, beleza?
A primeira é que estamos trabalhando com regime permanente, o ar e o hélio nós vamos considerar como sendo gases ideias, não ocorrem reações químicas no tubo e que a concentração de ar na tubulação e de hélio na atmosfera são desprezíveis… Feito isso, agora partiu ir pra resolução!
Temos um problema com dois grandes reservatórios de misturas de gases ideais ligados entre si por um canal e as concentrações das espécies em cada reservatório permanecem constantes… Ou seja, estamos trabalhando com contradifusão equimolar!
Vamos começar resolvendo a letra a! Ela quer a vazão mássica de hélio que vai para a atmosfera… Pra começar, vamos encontrar a área do nosso escoamento:
Com o diâmetro dado, vamos ter:
Nossas condições de contorno dizem que no fundo do tubo a pressão parcial de hélio é , isso quer dizer que:
E sabendo que no topo, em , a vazão molar é:
Substituindo os dados que temos:
Então a vazão mássica será:
Substituindo nossos valores:
Show! Partiu letra b!
Passo 2
Agora precisamos da fração mássica do ar que entra na tubulação, vamos nessa!!
Lembrando que em um processo de contradifusão equimolar temos que , então:
Opa! Então vamos achar a vazão mássica dentro da tubulação:
Então podemos encontrar a fração mássica de ar na tubulação, será:
Lembrando que a massa total será A vazão mássica total menos a vazão mássica em A e em B, vamos ter:
Opa! Isso significa que o ar no interior da tubulação é desprezível, ou seja, nossa suposição inicial se confirmou!
Passo 3
Agora só falta a letra c! Precisamos encontrar a velocidade média do escoamento no fundo do tubo… Para isso, vamos começar encontrando a vazão mássica líquida através do capilar:
Como a gente está considerando o hélio e o ar como gases ideais, podemos encontrar a densidade do hélio assim:
Beleza! Com esses dados podemos encontrar a velocidade com a relação:
Show de bola! Terminamos!