Um tubo de vidro vertical de de comprimento é preenchido até a metade com um líquido a . De quanto a altura da coluna de líquido variará quando o tubo for aquecido a ? Utilize:
(coeficiente de dilatação linear) (coeficiente de dilatação volumétrica)
Passo 1
Bom, galera, nesse problema a gente precisa descobrir quanto a altura de um líquido num frasco se altera quando esse líquido e o próprio frasco se expandem.
A ideia básica é a seguinte: O líquido vai se expandir, no entanto, nós vamos ter que “retirar” dessa expansão a própria expansão do frasco.
Por quê? Bem, pense numa bacia de água. Se você aquece a água, ela se expande e tende a sair pelas bordas da bacia. Porém, se o volume da bacia aumentar, essa água não vai mais transbordar, pois vai estar num recipiente maior. A ideia é bem intuitiva (:
Os físicos chamam esse fenômeno de dilatação aparente. A gente pode expressar essa ideia com essa fórmula:
Lembrando que é dado por:
Só que, como você deve ter percebido o problema não nos pede uma variação de volume, e sim uma variação de altura. Aliás o problema só nos dá o comprimento do frasco, e não o seu volume!
Bom, precisamos achar um modo de expressar essa variação de volume da fórmula acima em termos de . (:
Passo 2
Vamos imaginar que o nosso frasco tenha uma área de “boca” que vale . Veja a figura:
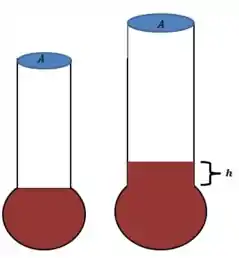
Sendo a figura da esquerda o frasco antes de ser aquecido e a figura da direita o frasco após ser aquecido, o que buscamos é o da figura! Considerando o trecho de comprimento cilíndrico, podemos escrever o volume desse trecho como:
Precisamos expressar os outros volumes usando também. Você vai ver que iremos cortar depois ;D :
Obs: Estamos considerando trechos cilíndricos!
Volume inicial do frasco:
Volume inicial do líquido: (Veja no enunciado que o líquido ocupa metade do volume no início).
Vamos, agora, enfim calcular !
Passo 3
Antes de partirmos para os cálculos, perceba que precisamos do coeficiente de dilatação volumétrica do vidro. Podemos calcular esse coeficiente, a partir da do coeficiente de dilatação linear, através da fórmula:
Vamos usar todas as informações que temos agora na fórmula da variação aparente:
Como a temperatura vai de a , . Substituindo tudo, enfim, na equação:
Cortando o de ambos os lados e calculando:
A altura negativa nos diz que o líquido desceu! Mas como estamos interessados em “quanto variará a altura”, podemos considerar apenas o módulo de :
(: