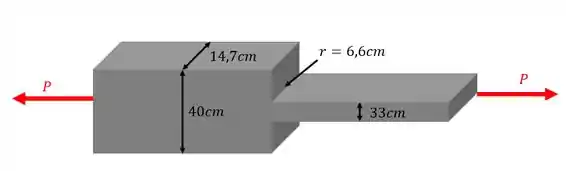
Uma barra de aço sofre uma redução de seção como mostra a figura. Sabendo que essa barra possui as dimensões mostradas no desenho e que a tensão normal admissível é de , determine a carga máxima que podemos aplicar nesta peça sem que ela rompa.
Passo 1
Pra resolver esse exercício vamos dividir a solução em 3 partes. Primeiro temos que lembrar qual é a nossa fórmula de tensão normal média
Em que
Aqui vale lembrar que usamos os valores da menor seção pois é nela que ocorrerá a maior tensão normal média, sempre lembre disso, usar os dados da menor seção, só usamos os valores da maior seção para definirmos o valor do coeficiente de concentração.
A segunda parte da nossa solução se trata de acharmos o coeficiente de concentração de tensão e para fazermos isso precisaremos de 3 coisas.
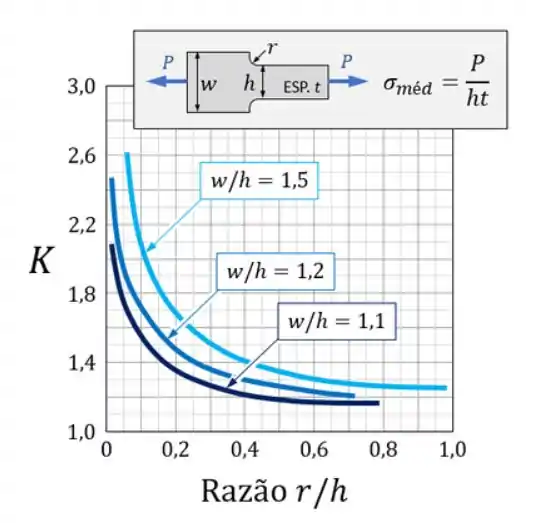
Primeiro usar um gráfico para determinar o coeficiente de concentração de tensão
Segundo devemos determinar qual a melhor curva do nosso gráfico para resolver o problema, e para isso usamos a relação
Em que no nosso caso se trata da relação entre as alturas da nossa peça como mostra a figura
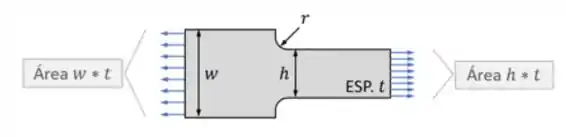
E por fim a terceira parte se trata de encontrarmos o valor no eixo horizontal do nosso gráfico, que encontraremos pela relação
Por fim a terceira parte da nossa solução será relacionar a tensão normal média com o coeficiente de concentração de tensão pela fórmula
Como queremos determinar o valor do carregamento máximo nessa parte final teremos que
Passo 2
Agora que já sabemos como calcular cada termo vamos a prática.
Como vimos a primeira parte da solução se trata de calcularmos a tensão Normal média pela fórmula
Em que sabemos que
E também já sabemos que se queremos determinar a maior tensão devemos usar a menor área
Com isso teremos que
Logo teremos
Passo 3
Vamos agora determinar o coeficiente de concentração de tensão.
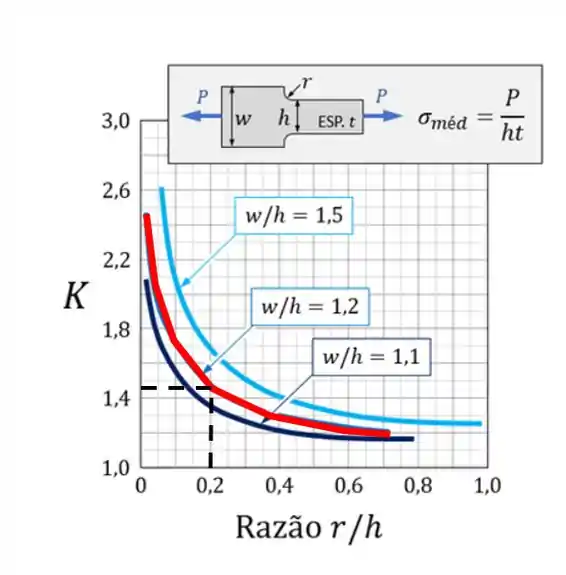
Sabemos que primeiro devemos usar um gráfico, que é esse aqui
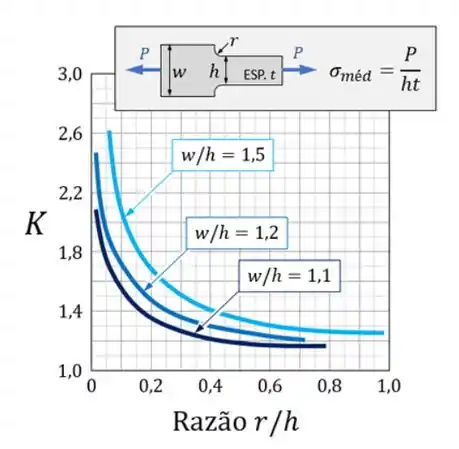
Depois devemos determinar a melhor curva pela relação
Agora que já sabemos a melhor curva só falta determinar o valor horizontal, que determinamos pela fórmula
Agora vamos determinar o valor do K
Passo 4
Agora basta relacionarmos a nossa tensão Normal média com o coeficiente de concentração de tensão pela fórmula
Sabemos que
Substituindo na nossa fórmula teremos que
Com isso descobrimos que