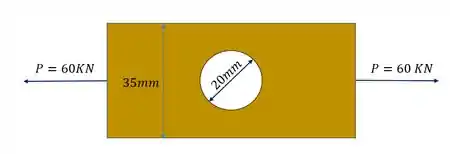
Uma chapa furada foi submetida ao carregamento mostrado abaixo, sabendo que ocorrerá concentração de tensões, determine a tensão máxima normal ao qual essa chapa será submetida. Espessura da barra de 5mm. Explique o que ocorreria se a resistência a tensões normais dessa peça fosse de 1600Mpa.
Passo 1
Essa questão se trata de uma questão de concentração de tensão. O que temos que ter em mente é que essa questão se divide em duas fases de resolução.
A primeira se trata de determinarmos o valor da tensão média, como se trata de uma chapa furada devemos usar a seguinte fórmula para calcula-la.
Em que cada uma das letras está indicada na figura abaixo
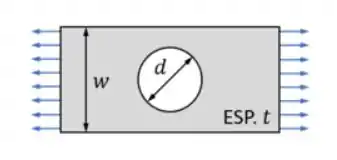
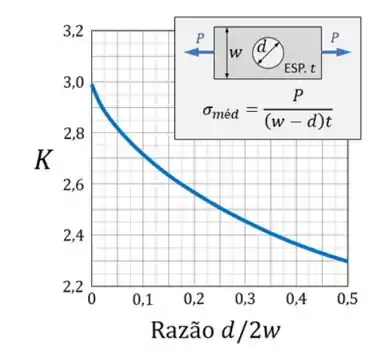
A segunda parte da solução se concentra em determinar o valor de K, ou seja, do concentrador de tensões. Para determinar o valor de K também seguimos um passo a passo. Já sabemos que para furos temos apenas uma curva, precisamos então determinar o valor horizontal do nosso eixo. Para fazermos isso usamos a fórmula
Com o valor horizontal e com a curva determinamos facilmente o valor do K.
Por fim para encontrarmos o valor da tensão normal máxima quando tem concentração de tensão basta multiplicarmos a tensão média pelo concentrador de tensões.
Passo 2
Vamos então a primeira parte da solução, que é determinar o valor da tensão média, para isso devemos comparar a nossa peça com o nosso formato base
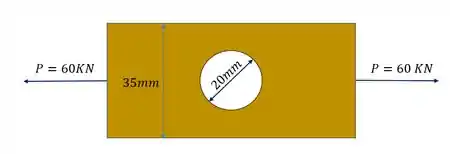
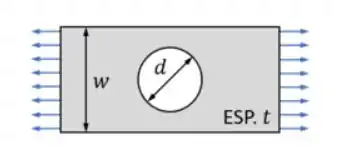
Então podemos definir que
Como a nossa fórmula é
Basta substituir os valores na nossa equação
Passo 3
Agora que já sabemos o valor da tensão média, devemos determinar o valor do nosso K, ou seja, do concentrador de tensão, para isso devemos primeiro determinar o valor horizontal, usando a nossa fórmula teremos que
Com o valor horizontal devemos analisar a nossa curva
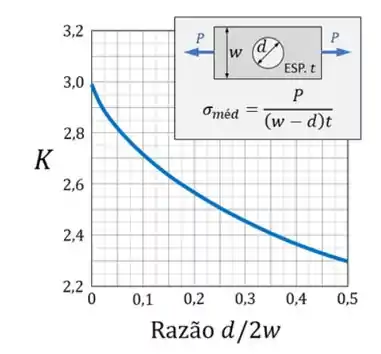
Vamos marcar qual seria o nosso provável valor de K
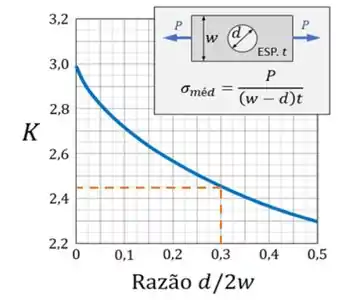
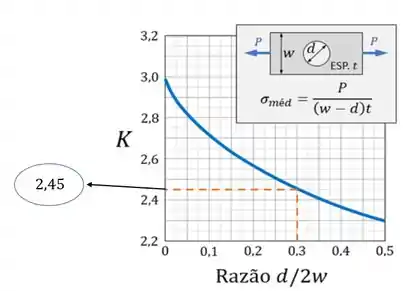
Podemos então definir que
Passo 4
Agora vamos para a ultima parte da questão, que devemos apenas multiplicar o valor da tensão média que calculamos pelo coeficiente de concentração de tensão que calculamos também, podemos então definir a nossa tensão normal máxima como
Substituindo teremos que
Isso é de suma importância ser avaliado, pois veja que o valor da tensão normal máxima é maior que o dobro da tensão média, isso explica por exemplo, porque é perigoso fazer furos em vigas, a concentração de tensões pode acabar com a resistência dela.
Pense no seguinte, imagine que a resistência a tensão normal da nossa viga fosse de 1600 Mpa.
Quando calculamos a tensão média, vemos que é metade da tensão admissível. Agora se você fizer o furo como o da figura, verá que a tensão máxima é de 1960 Mpa, maior que a tensão admissível, logo, ocorre o rompimento da barra.
Resposta
Analisando os esforços vemos que
Logo, ocorre o rompimento.