Determine a força axial máxima que pode ser aplicada à barra. A barra é feita de aço e tem tensão admissível .
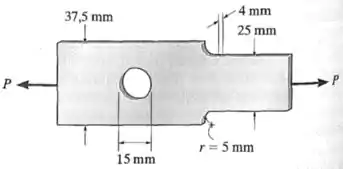
Observação: Use os gráficos abaixo para determinar os coeficientes de concentração de tensão :
Passo 1
O que está acontecendo?
A barra tem uma espessura e está submetida a uma força axial de tração , que gera ao longo dela uma força interna normal .
A tensão normal nessa barra vai ser máxima em um dos dois concentradores de tensões existentes.
O primeiro concentrador de tensões é um furo de diâmetro em uma região de largura .
Originalmente, a área da seção transversal dessa região era igual à largura vezes a espessura .
Mas por causa do furo de diâmetro , a largura efetiva da seção transversal que passa bem no meio do furo vai ser igual à .
Dessa forma, a área dessa seção vai ser:
Com isso, a tensão normal média nessa seção vai ser igual à:
Mas essa é só a tensão normal média.
Também por causa do furo, vai haver uma concentração de tensões de tal forma que a tensão normal máxima nessa região vai ser:
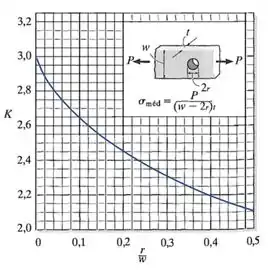
Onde é um coeficiente que pode ser encontrado no gráfico abaixo inserindo o valor da razão (onde é o raio do furo, que igual à metade de seu diâmetro ):
Já o segundo concentrador de tensões é o adoçamento de raio entre uma região menor de largura e uma região maior de largura .
Na região desse concentrador de tensões, a maior tensão normal média vai ser a que ocorre na região com a largura menor .
Nessa região, vamos ter uma área de seção transversal igual à largura vezes a espessura , de tal forma que:
Mas mais uma vez, essa é só a tensão normal média. A tensão normal máxima vai ser:
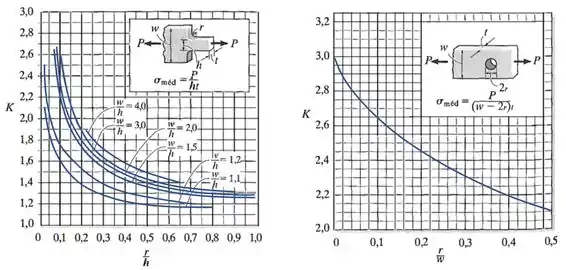
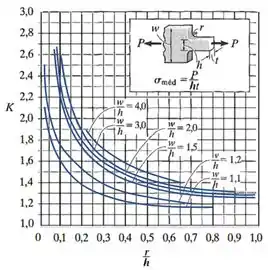
Onde é um coeficiente que deve ser encontrado inserindo as razões e no gráfico abaixo:
E o que é que o exercício quer?
Ele quer que a gente descubra o valor máximo admissível da carga tendo em mente que o material possui uma tensão admissível .
Para descobrir isso, vamos ter que aplicar, para cada um dos dois concentradores de tensões, a condição de projeto:
Desenvolvendo essa condição de projeto, vamos poder encontrar a carga máxima de acordo com cada concentrador de tensões.
O valor máximo admissível de para a barra como um todo vai ser o menor dos valores máximos de que forem encontrados para cada concentrador de tensão.
Passo 2
Então vamos começar estudando o primeiro concentrador de tensões: o furo.
Começamos aplicando a condição:
Substituindo , temos:
E substituindo a fórmula da tensão normal média , temos:
Aqui, sabemos:
- Que a força interna normal em toda a barra é igual à carga axial ;
- E que, como vimos no Passo 1, a área da seção transversal da região do furo é igual à .
Substituindo esses valores, temos que:
Queremos encontrar o valor máximo da carga , então devemos isolá-la:
Nessa expressão, só não conhecemos o valor do coeficiente .
Então vamos encontrá-lo!
Passo 3
Para encontrar o valor do coeficiente para esse furo, vamos olhar para o seu gráfico:
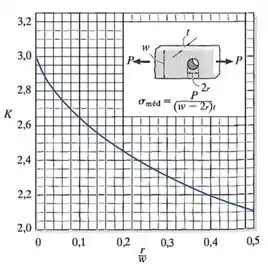
Vemos que para encontrar , precisamos conhecer o valor da razão .
O nosso furo tem um diâmetro , então ele tem um raio .
Como a região do furo tem uma largura , então a razão vai ficar assim:
Inserindo esse valor no gráfico:
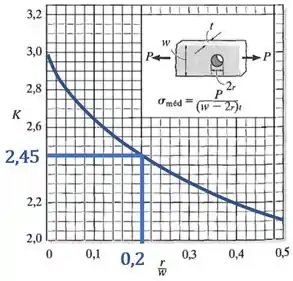
Encontramos que o coeficiente de concentração de tensões para esse furo é:
Passo 4
Agora que sabemos o valor de , podemos voltar para a expressão que tínhamos encontrado para a carga :
Substituindo os valores:
- ;
- , e ;
- & ,
- ;
- e ;
- & ,
Encontramos que:
Ou seja, de acordo com a concentração de tensões no furo, a carga máxima admissível é:
Passo 4
Em seguida, vamos estudar o segundo concentrador de tensões: o adoçamento.
Começamos aplicando a condição:
Substituímos e , encontrando que:
Aqui, sabemos que a força interna normal em toda a barra é igual à carga axial .
Além disso, queremos estudar o lado do adoçamento com a menor área de seção transversal, que é a região com a largura menor e com a área menor .
Então temos que:
Queremos encontrar a carga máxima, então devemos isolá-la:
Nessa expressão, só não conhecemos o valor de , então vamos encontrá-lo!
Passo 5
Para encontrar o valor do coeficiente para esse adoçamento, vamos olhar para o seu gráfico:
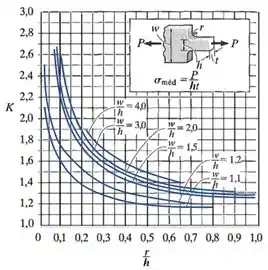
Vemos que para encontrar , precisamos conhecer o valor das razões e .
Calculando essas razões, encontramos que:
Selecionando a curva para e inserindo o valor da razão no gráfico:
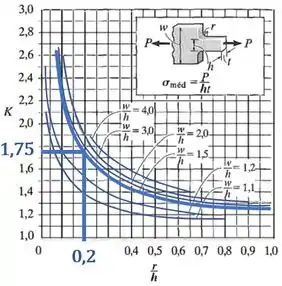
Encontramos que:
Passo 6
Agora que conhecemos , voltamos para a expressão encontrada para a carga :
Substituindo os valores:
Encontramos que:
Ou seja, de acordo com a concentração de tensões no adoçamento, a carga máxima admissível é:
Vemos que a carga máxima admissível para o furo é menor.
Então para garantir a segurança das regiões do furo e do adoçamento, deve ser a carga máxima admissível para toda a barra.
Ou seja, a força axial máxima que pode ser aplicada à barra é: