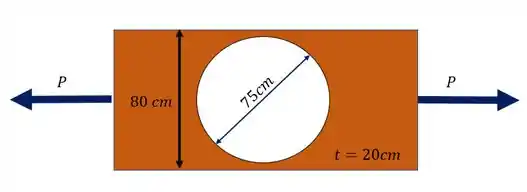
Determine a máxima carga que pode ser aplicada na peça abaixo que possui uma seção furada. Para isso use . Todas as dimensões são dadas na figura.
Passo 1
Pra resolver esse exercício vamos dividir a solução em 3 partes. Primeiro temos que lembrar qual é a nossa fórmula de tensão normal média, lembrando que para seções furadas no temos que
Em que
Em que cada uma das letras está indicada na figura abaixo
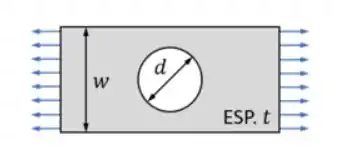
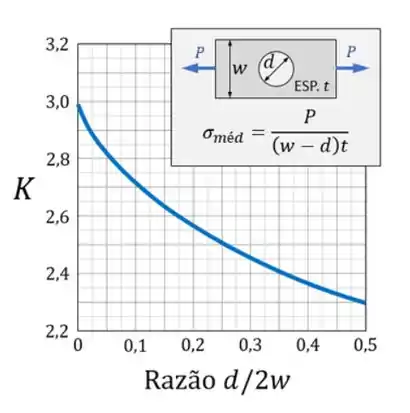
A segunda parte da solução se concentra em determinar o valor de K, ou seja, do concentrador de tensões. Para determinar o valor de K também seguimos um passo a passo. Já sabemos que para furos temos apenas uma curva, precisamos então determinar o valor horizontal do nosso eixo. Para fazermos isso usamos a fórmula
Com o valor horizontal e com a curva determinamos facilmente o valor do K.
Por fim para encontrarmos o valor da tensão normal máxima quando tem concentração de tensão basta multiplicarmos a tensão média pelo concentrador de tensões.
Vale lembrar também que como queremos determinar o valor do carregamento máximo nessa parte final teremos que
Passo 2
Agora que já sabemos como calcular cada termo vamos a prática.
Como vimos a primeira parte da solução se trata de calcularmos a tensão Normal média pela fórmula
Em que sabemos que
Logo teremos
Passo 3
Vamos agora determinar o coeficiente de concentração de tensão.
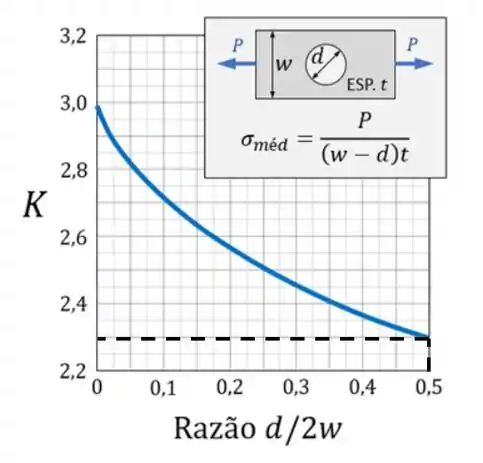
Sabemos que primeiro devemos usar um gráfico, que é esse aqui
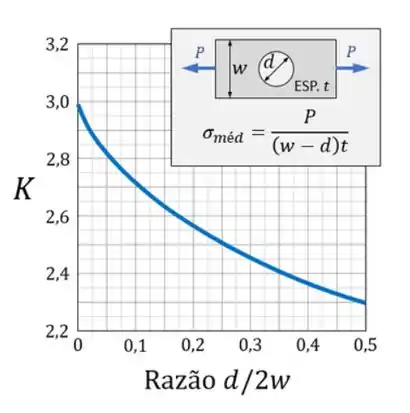
Agora devemos primeiro determinar o valor horizontal, usando a nossa fórmula teremos que
Com o valor horizontal devemos analisar a nossa curva
Agora vamos determinar o valor do K
Passo 4
Agora basta relacionarmos a nossa tensão Normal média com o coeficiente de concentração de tensão pela fórmula
Sabemos que
Substituindo na nossa fórmula teremos que
Com isso descobrimos que