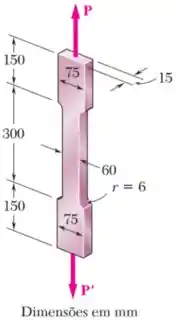
O corpo de prova de alumínio mostrado está submetido a duas forças iguais axiais, opostas e centradas de intensidade . Sabendo que e , determine o máximo valor admissível de e o correspondente alongamento total do corpo de prova. Resolva a parte , considerando que o corpo de prova foi substituído por uma barra de alumínio de mesmo comprimento e seção retangular uniforme de .
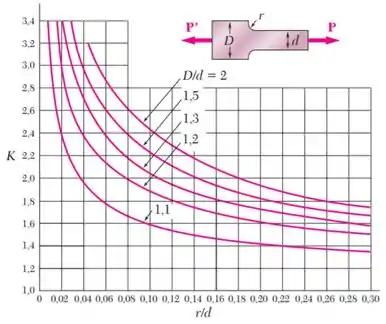
Observação: Use o gráfico abaixo para determinar o coeficiente de concentração de tensão :
Passo 1
O que está acontecendo?
O corpo de prova é composto por três segmentos:
- Dois segmentos iguais nas extremidades, cada um com um comprimento e uma área de seção transversal ;
- E um segmento central de comprimento e área de seção transversal ;
Além disso as forças de tração geram ao longo de todo o corpo de prova uma força interna normal .
Essa força normal gera nos diferentes segmentos do corpo tensões normais médias e variações de comprimento :
Agora, vai haver uma concentração de tensões nos adoçamentos de raio entre as regiões de largura e do corpo.
Por causa dessa concentração de tensões, a tensão normal máxima no corpo vai ser:
Onde:
- deve ser calculada para a região com a menor área de seção transversal (a região central de área );
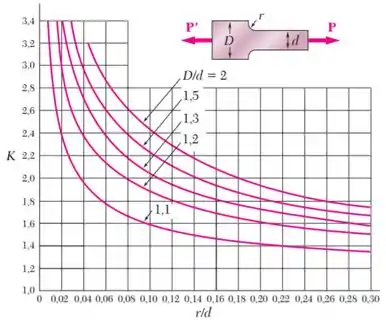
- E é um coeficiente que deve ser determinado usando o gráfico fornecido:
O corpo de prova é feito de um alumínio com módulo de elasticidade e tensão admissível .
E o que é que o exercício quer?
No item , ele quer que a gente determine o valor máximo admissível de nesse corpo de prova e a variação de comprimento correspondente.
O valor máximo admissível de é aquele em que a tensão máxima na peça ainda é menor ou igual à tensão admissível, ou seja:
Já a variação de comprimento vai ser a soma das variações de comprimento de cada um dos dois segmentos iguais com a variação de comprimento do segmento central:
Já no item , ele quer saber mais uma vez o valor máximo admissível de e a variação de comprimento correspondente.
Mas dessa vez supondo que o corpo é feito de um segmento só de comprimento e área de seção transversal .
Como não vai haver concentração de tensões, a tensão máxima na peça vai ser a própria tensão normal média, e a condição que vamos usar para encontrar vai ser:
Já a variação de comprimento vai ser encontrada usando a mesma fórmula de sempre:
Passo 2
Então primeiro, para encontrar a força máxima admissível no corpo de prova original do item , vamos aplicar a condição:
Substituindo e , temos que:
Sabemos que a força interna normal em toda a peça é igual à tração .
E sabemos que deve ser calculada para a região com a menor área de seção transversal (a região central de área ).
Tendo isso em mente, a nossa condição fica assim:
Queremos encontrar a força máxima, então devemos isolá-la:
Agora, antes de prosseguirmos, precisamos determinar o valor do coeficiente .
Passo 3
Para encontrar , vamos olhar para o seu gráfico:
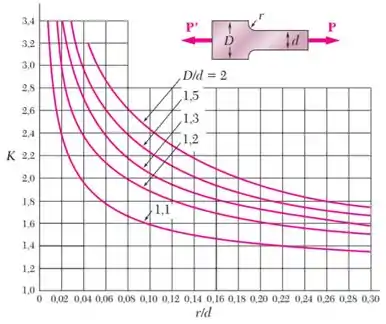
Vemos que precisamos definir a razão entre as larguras e a razão entre o raio de adoçamento e a largura menor .
Calculando essas razões, encontramos que:
E que:
Agora, quando vamos tentar escolher a curva do gráfico para , vemos que essa curva não existe.
Então vamos ter que encontrar um valor aproximado para : vamos fazer a média entre os valores encontrados usando as curvas mais próximas e .
Inserindo no gráfico a razão , encontramos que para a curva , , e que para a curva , .
Assim, podemos aproximar que, para o nosso caso, o coeficiente de concentração de tensões vai ser:
(Esse é o valor necessário para encontrar o gabarito do exercício, mas, se você tiver estimado outro valor próximo, a sua resposta também estará certa!)
Passo 4
Voltando para a expressão que tínhamos encontrado para a força máxima no corpo de prova:
E substituindo:
- ;
- ;
- E ,
Encontramos que:
Ou seja, o valor máximo admissível da força nesse corpo de prova é .
Passo 5
Agora, podemos usar o valor encontrado para para determinar a variação de comprimento correspondente no corpo de prova.
Primeiro, sabemos que vai ser a soma das variações de comprimento de cada um dos dois segmentos iguais com a variação de comprimento do segmento central:
Esses segmentos têm a mesma força normal e o mesmo módulo de elasticidade , mas comprimentos e áreas de seção transversal diferentes.
Então aplicando a fórmula para esses segmentos, vamos ter:
Colocando em evidência, temos:
E como a força normal em toda a peça é igual à tração , temos que:
Substituindo nessa expressão os valores:
- ;
- ;
- e ;
- & e ,
Encontramos que:
E assim terminamos o item !
Passo 6
Em seguida, para encontrar a força máxima admissível no corpo de prova modificado do item , vamos aplicar a condição:
Substituindo a fórmula da tensão normal média, temos:
Como a força normal ao longo de todo o corpo de prova é igual à tração , temos que:
Queremos encontrar a força máxima, então devemos isolá-la:
Como o corpo de prova modificado do item vai ter uma única área de seção transversal , podemos substituir essa área aqui.
Fazendo essa substituição e substituindo também , encontramos que:
Ou seja, a força máxima admissível no corpo de prova do item é .
Passo 7
Por fim, para encontrar a variação de comprimento correspondente no corpo de prova do item , usando a fórmula:
Substituindo nela os valores:
- ;
- ;
- ;
- & ,
Encontramos que:
E assim finalizamos o item e o exercício como um todo!