Essa atividade consiste em resolver a equação diferencial que representa a dinâmica de um sistema massa-mola-amortecedor não linear. Um sistema massa mola-amortecedor não linear é representado pelas seguinte equação diferencial:
Onde é a posição da massa e é a força aplicada na massa.
Simule o sistema para a condição inicial e e para a força variando na forma de um degrau de amplitude igual a , no intervalo de tempo entre e segundos. Apresente os gráficos da posição, velocidade e força.
Passo 1
Neste exercício, resolveremos uma equação diferencial de 2ª ordem não-linear usando o SIMULINK. Apesar de a equação ser não-linear, a dica de isolar a derivada de maior ordem ainda está valendo:
Desta forma, identificamos onde colocaremos os dois blocos “Integrator” que precisamos para encontrar (usaremos um bloco “Integrator” para integrar e obter ; e outro “Integrator” que receberá o , o integrará e nos dará ) e por onde começamos a construir o diagrama de blocos.
O enunciado pede para plotarmos os gráficos da posição, da velocidade e da força, ou seja, os gráficos de , e , respectivamente. Para gerarmos os gráficos pedidos pelo enunciado, usaremos três blocos “Scope”, uma para cada gráfico.
Passo 2
Vamos começar o diagrama pelo lado direito da equação: , mais especificamente por . é um degrau de amplitude , por isso, em um modelo novo, insira um bloco “Step” e altere sua propriedade “Final value” para .
Em seguida, insira um bloco “Add” e troque sua propriedade “List of signs” de por , para que “Add” tenha três entradas, uma com sinal as outras duas com sinal . Conecte o “Step” à entrada positiva de “Add”:

As outras duas entradas de “Add” receberão e , portanto, a saída de “Add” será igual a , que é igual a . Logo, a saída de “Add” será e é nele que devemos conectar um bloco “Integrator”.
Passo 3
Insira um bloco “Integrator” no modelo e conecte sua entrada à saída de “Add”:
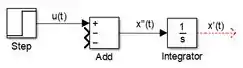
Este bloco “Integrator” integrará e nos dará . Como , não precisamos alterar a propriedade “Initial condition” de “Integrator”, pois por padrão ela já é igual a .
Para obter , insira outro bloco “Integrator” e conecte sua entrada à saída do primeiro bloco “Integrator”. Em outras palavras, o segundo bloco “Integrator” receberá , o integrará e fornecerá . Como , mude a propriedade “Initial condition” do “Integrator” que calculará (destacado abaixo) para esse valor:
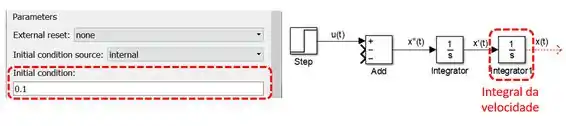
Para gerar o gráfico de , insira um bloco “Scope” e conecte-o ao “Integrator” que calcula a posição :
Passo 4
Precisamos terminar de modelar o lado direito da equação: . Vamos começar por . Para calcular , insira um bloco “Product” e faça com que suas duas entradas recebam , conectando cada entrada à flecha entre os dois blocos “Integrator” (que corresponde ao sinal de ):
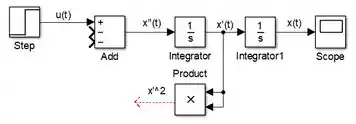
Em seguida, insira um bloco “Gain”, faça com que seu ganho seja igual a e conecte sua entrada à saída de “Product”. Conecte a saída de “Gain” com uma das entradas negativas de “Add”. Dessa forma, já temos :
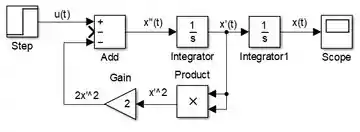
Passo 5
Vamos modelar o termo . Para calcular , usaremos o bloco “Math Function”, da biblioteca “Math Operations”:
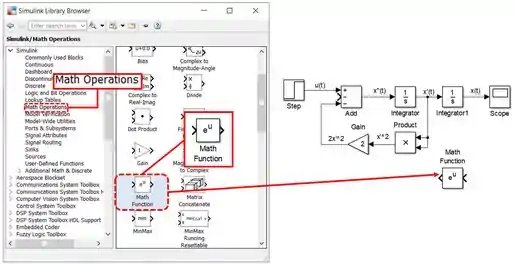
Este bloco aplica uma função matemática em sua entrada e retorna o resultado. Ele inclui funções como exponenciação, módulo e, o que interessa pra gente, logaritmo. Para calcular , conecte a entrada do bloco “Math Function” à flecha entre “Integrator1” e “Scope” (que representa o sinal de ) e altere a propriedade “Function” do bloco “Math Function” para :
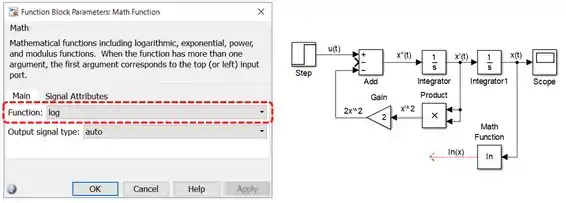
No SIMULINK, assim como no MATLAB, o logaritmo natural, isto é, o , é representado por . Quando queremos calcular o logaritmo na base de algum número, usamos (repare que tem essa opção também no prâmetro “Function”).
Quando você fizer a alteração, note que o bloco “Math Funtion” muda de cara, passando a ter um dentro dele.
Para terminar o termo , insira outro bloco “Gain” e faça com que seu ganho seja igual a . Em seguida, conecte a entrada de “Gain” com ganho à saída de “Math Function” e sua saída, à entrada negativa restante de “Add”:
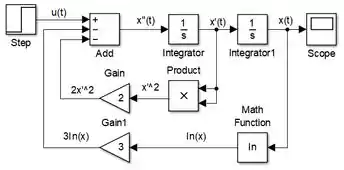
Pronto! A equação diferencial está modelada!
Passo 6
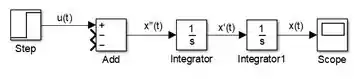
No diagrama atual, conseguimos apenas gerar o gráfico de . Para plotar e , insira mais dois blocos “Scope” e conecte um ao sinal de e outro ao sinal de :
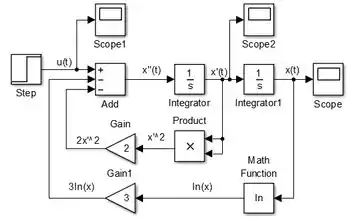
O enunciado pediu para simularmos o sistema de a , que já é o tempo de simulação padrão do SIMULINK. Por isso, não precisamos alterá-lo e já podemos executar o programa para vermos os gráficos de , e .
Resposta
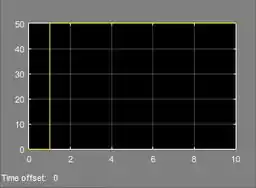
Gráfico da posição
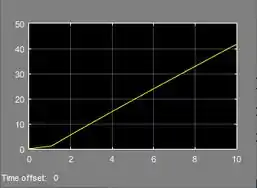
Gráfico da velocidade
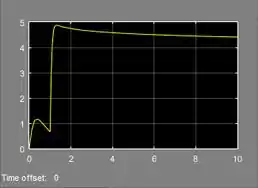
Gráfico da força