A seguinte equação descreve ao temperatura de um certo objeto imerso em um líquido com temperatura constante .

Suponha que a temperatura inicial do objeto é e a temperatura do líquido é. Utilizando o SIMULINK:

1. Plote a temperatura do objeto em função do tempo;
2. Em quanto tempo a temperatura do objeto atingirá a temperatura do líquido?

Vamos começar modelando a diferença . Em um novo modelo do SIMULINK, insira um bloco “Constant” e faça com que seu valor seja igual a . Em seguida, insira um bloco “Add” e altere seus parâmetros, de forma que ele tenha um entrada positiva e outra negativa:

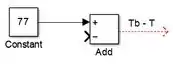
O bloco “Add” receberá o sinal de mais para frente, por isso, a saída de “Add” será .

Para termos , insira um bloco “Gain”, faça com que seu ganho seja igual a e conecte sua entrada à saída de “Add”:

A saída de “Gain” será . E quem é igual ? É ! Por isso, a saída de “Gain” será igual à derivada da nossa EDO.

Isso significa que temos que adicionar um bloco “Integrator” à direita de “Gain” e conectar a saída de “Gain” à entrada de “Integrator”. Desta forma, “Integrator” nos dará . Não esqueça de mudar o parâmetro “Initial condition” de “Integrator” de para , pois .

Para termos o gráfico de , insira um bloco “Scope” e conecte-o a “Integrator”:

Para finalizar o modelo, leve o sinal de até a entrada negativa de “Add”:

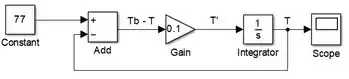
A EDO está modelada! Vamos ver o gráfico de , executando a simulação e clicando duas vezes sobre “Scope”:

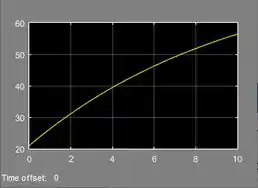
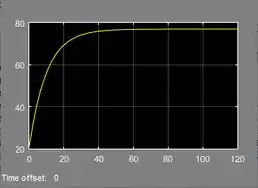
Rodei a simulação para . Contudo, note que o eixo vertical do gráfico vai só até e na letra queremos saber quanto tempo o objeto demora para atingir a temperatura do líquido, isto é, . Temos que aumentar o tempo de simulação para que a curva do gráfico atinja essa temperatura. Aumente o tempo para :

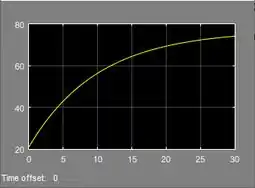
Agora o eixo vertical vai até , pode ser que agora encontremos a temperatura de .

Para vermos os valores da curva, na janela do “Scope”, clique em “Try Time Scope” e o use o “Cursor Measurements”:

Leve o cursor até o início da curva, onde teremos (destacado em amarelo abaixo). Arraste o cursor até o final da curva para vermos a temperatura do objeto em (destacado em vermelho abaixo).

Note que e queremos saber o tempo que demora para que o objeto tenha um temperatura igual a . Por isso, devemos aumentar o tempo de simulação até que consigamos que o cursor nos retorne um valor igual ou muito próximo de .

Sem fechar a janela do “Scope” com o gráfico e os cursores, aumente o tempo de simulação e rode o programa novamente. O gráfico se atualizará automaticamente. Faça esse procedimento até que o cursor retorne .

Eu fui aumentando o tempo de simulação até , quando finalmente encontrei o valor (destacado em vermelho abaixo):

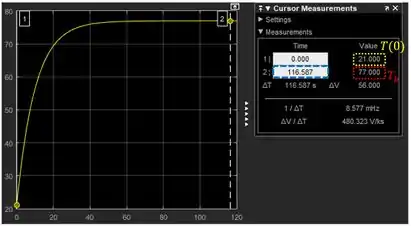
O tempo que o objeto demora para que sua temperatura atinja é dado pelo campo destacado em azul acima: .