A seguinte equação não tem solução analítica embora seja linear.
,
A solução aproximada, que é pouco precisa para valores altos de , é:
Crie um modelo no SIMULINK para resolver esse problema, e compare a solução com a solução aproximada em .
Passo 1
Neste exercício, vamos solucionar a EDO usando o SIMULINK e vamos comparar a solução com a solução aproximada.
Para resolver uma equação diferencial pelo SIMULINK, a dica é “isolar” a derivada da EDO. Por isso, vamos rearranjar a EDO para:
Desta forma, podemos imaginar: “a derivada é igual a quê?”, localizando onde colocaremos o bloco “Integrator” que nos dará .
Vamos enviar a solução da EDO para um bloco “To Workspace”, para que possamos plotar o resultado junto com a solução aproximada usando o Command Window do MATLAB.
Passo 2
Sabemos que a derivada é igual a , por isso, vamos começar montando o lado direito da equação. Para criar o termo , vamos precisar de dois blocos novos: um bloco “Clock” e um bloco “Trigonometric Function”.
Vá à biblioteca “Sources”, encontre o bloco “Clock” e insira-o em um novo modelo. O bloco “Clock” fornece o tempo de simulação, de forma que podemos usá-lo para construir funções dependentes do tempo. Em outras palavras, ele representará o de .

O bloco “Trigonometric Function” pertence à biblioteca “Math Operations” e ele calcula a função trigonométrica de seu sinal de entrada. Insira um desses blocos no modelo e conecte sua entrada à “Clock”:

Para transformar o “Trigonometric Function” em uma função tangente, clique duas vezes sobre ele para acessar suas propriedades. A propriedade “Function”, destacada abaixo, contém uma lista de funções trigonométricas. Selecione a opção tan e clique em “OK”.
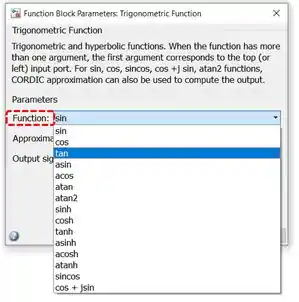
Note que o bloco “Trigonometric Function” mudou de cara:

Passo 3
Para fazer a diferença , insira um bloco “Add” e altere o parâmetro “List of signs” (destacado abaixo), para que uma das entradas de “Add” tenha um sinal negativo, para receber o . Conecte a saída de “Trigonometric Function” à entrada com sinal de “Add”:

Faremos com que a saída de “Add” seja igual a . E é igual a o quê? A ! E é que devemos integrar para encontrar . Por isso, insira um bloco “Integrator”, pertencente à biblioteca “Continuous”, à direita de “Add” e conecte sua entrada à saída de “Add”, como na figura abaixo:

Como a condição inicial da EDO é nula, não precisamos mexer nos parâmetros de “Integrator”, pois o padrão do bloco é ter condição inicial nula.
Passo 4
A saída de “Integrator” será , a solução da nossa EDO. Como queremos gerar o gráfico dela no MATLAB (pois ficará mais fácil de plotar a solução encontrada no SIMULINK com a solução aproximada), vamos inserir um bloco “To Workspace”. Este bloco serve para levar para o “Workspace” do MATLAB os resultados da simulação, permitindo manipulá-los no “Command Window”. Conecte a saída de “Integrator” a entrada de “To Workspace”:
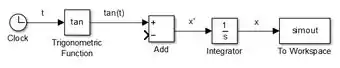
Se você quiser, você pode alterar o nome da variável que receberá o resultado da simulação no “Workspace” do MATLAB, clicando duas vezes sobre o bloco “To Workspace” e mexendo na propriedade “Variable name”. Eu fiz com que minha variável se chamasse .
Agora que temos , podemos fechar nosso diagrama, conectando a entrada com sinal de de “Add” com a seta entre “Integrator” e “To Workspace”:

Passo 5
Troque o tempo de simulação para e rode o programa. Vá ao MATLAB e olhe o “Workspace”. Você verá que apareceram duas variáveis: e , que estão aí graças ao bloco “To Workspace”. é um vetor que contém o tempo de simulação, indo de a . Já contém o resultado da simulação do SIMULINK.
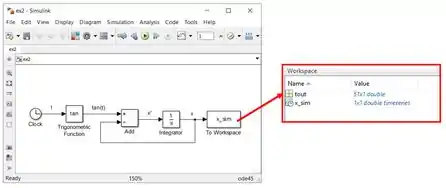
Para gerar o gráfico com a solução da EDO obtida pelo SIMULINK e a solução aproximada, abra um script novo no MATLAB e digite as seguintes linhas de código:
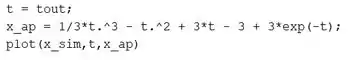
Na primeira linha, criamos um vetor igual ao vetor .
Na segunda linha, calculamos para cada elemento do vetor e armazenamos o resultado no vetor .
Finalmente, na última linha, plotamos as curvas da solução obtida pelo SIMULINK e da solução aproximada. Execute o script e você terá o gráfico.
Quando você executar o programa, o MATLAB vai te pedir para salvar o script. Se for salvá-lo na mesma pasta onde está o arquivo do seu modelo SIMULINK, dê um nome diferente, para não haver conflito.
Resposta

A curva azul é a solução obtida pelo SIMULINK e a curva vermelha, a solução aproximada.