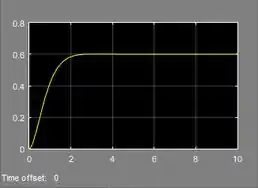
Modele a seguinte equação diferencial e observe o gráfico:
Passo 1
Neste exercício, vamos resolver uma EDO de segunda ordem pelo SIMULINK. Comece pela dica de isolar a derivada de maior ordem da EDO:
Desta forma, fica mais fácil identificar onde colocaremos o bloco “Integrator” (nesse caso, utilizaremos dois, pois a EDO tem uma segunda derivada) e qual bloco da biblioteca “Sources” utlizaremos para começar a construir o modelo.
O primeiro bloco “Integrator” nos dará e o segundo, , que é a solução da EDO.
Ao final, geraremos o gráfico de usando um bloco “Scope”.
Passo 2
Vamos começar modelando o lado direito da EDO: . O pode ser modelado por um bloco “Constant”, da biblioteca “Sources”, e as operações de subtração serão feitas por meio de um bloco “Add”.
Faça com que o bloco “Constant” seja igual a . Por padrão, o bloco “Add” possui duas entradas positivas. Altere seus parâmetros para que ele passe a ter uma entrada positiva e duas negativas, trocando o por no parâmetro “List of signs”:

Conecte “Constant” à entrada positiva de “Add”. As entradas negativas de “Add” receberão e mais para frente, por isso, a saída de “Add” será .
Passo 3
Para obter , insira um bloco “Integrator” e conecte a saída de “Add” à entrada deste bloco. Desta forma, estaremos integrando para gerar .
![]()
Como , não precisamos alterar o parâmetro “Initial condition” de “Integrator”, pois as condições iniciais são nulas por padrão.
Agora que temos , vamos inserir mais um bloco “Integrator” para obter . Coloque-o à direita do primeiro “Integrator” inserido e conecte-os:

Novamente, não precisamos mudar os parâmetros do segundo “Integrator” inserido, pois e por padrão as condições iniciais de “Integrator” são nulas.
Insira um bloco “Scope” e conecte sua entrada à saída de “Integrator1”, para que tenhamos o gráfico de .

Passo 4
Vamos terminar de modelar o lado direito da EDO: , começando por . Insira um bloco “Gain” no modelo e altere seu ganho para . Em seguida, conecte sua entrada à flecha entre os dois blocos “Integrator” (pois é ali que temos o sinal representando ) . Conecte a saída de “Gain” a uma das entradas negativas de “Add”:

Para modelar , o procedimento é igualzinho. Insira outro bloco “Gain” e mude o ganho para . Então, conecte a entrada desse “Gain” igual a à flecha conectando o bloco “Integrator1” a “Scope”, pois é onde temos o sinal de . Para finalizar o modelo, conecte a saída de “Gain1” à última entrada negativa de “Add”:

Voilà! EDO modelada! Para ver o gráfico de , basta rodar a simulação.
Resposta