O nível de um tanque de área de seção transversal , com uma válvula de saída com resistência , é dado por:
Onde representa a vazão de entrada.
Usando o SIMULINK, encontre , sabendo que inicialmente o tanque está com um nível . Considere , e que a vazão de entrada equivale a uma função degrau onde .
Passo 1
Usaremos o SIMULINK para encontrar a solução da equação diferencial do enunciado e plotar seu gráfico. A solução é e corresponde ao nível de um tanque em função do tempo, em horas.
A equação diferencial dada pelo enunciado já está com a derivada isolada no lado esquerdo, facilitando o raciocínio: “a derivada é igual a o quê?”, nos ajudando a identificar onde pôr o boco “Integrator” que nos dará . A saída de “Integrator” será conduzida a um bloco “Scope”, que nos dará o gráfico de .
Passo 2
Vamos atualizar a equação diferencial com as constantes dadas no enunciado:
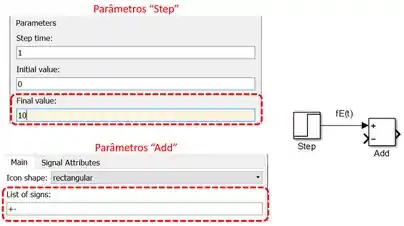
Vemos que a derivada é igual a , por isso, vamos começar modelando o lado direito da equação. Em novo modelo do SIMULINK, insira um bloco “Step” (representando ) e um bloco “Add”. Para o bloco “Step”, mude o parâmetro “Final value” para (destacado), para ele ter o valor da vazão de entrada.
No bloco “Add”, altere o parâmetro “List of signs” (destacado abaixo), para que uma das entradas de “Add” tenha um sinal negativo, para receber o mais pra frente. Conecte a saída de “Step” à entrada com sinal de “Add”:
Passo 3
A saída de “Add” será a diferença . Para que esta diferença seja igual a , ele deve ser multiplicada por . Por isso, vamos colocar um bloco “Gain” à direita de “Add”, fazer com que seu ganho seja igual a e conectar sua entrada à saída de “Add”:
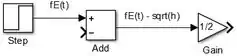
A saída de “Gain” será a derivada , por isso, vamos inserir um bloco “Integrator” à sua direita e conectá-los. Altere o parâmetro “Initial Condition” de “Integrator” para :

Passo 4
A saída de “Integrator” é a solução da equação diferencial . Para gerarmos o seu gráfico, insira um bloco “Scope” e conecte-o a “Integrator”:

Agora que temos , podemos criar o termo da diferença . Para isto, vamos usar um bloco novo, o “Sqrt”, da biblioteca “Math Operations”, que calcula a raiz quadrada de um sinal.

Insira-o no modelo e conecte sua entrada à seta entre o bloco “Integrator” e “Scope”:

Dessa forma, o sinal de vai simultaneamente para “Scope” e para “Sqrt”. “Sqrt” vai nos dar em sua saída , por isso, conecte a saída de “Sqrt” à entrada negativa do bloco “Add”, para obtermos :

O diagrama de blocos representando a equação diferencial está pronto! Para vermos o gráfico de , execute o programa. Como o enunciado não especificou o tempo da simulação, faremos com que seja o padrão de mesmo. Em seguida, clique duas vezes sobre “Scope” para ver o gráfico.
Resposta
