Considere o circuito elétrico abaixo:
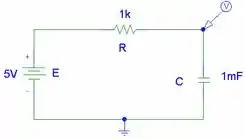
O circuito possui um resistor e um capacitor em série alimentados por uma fonte constante. O capacitor possui tensão inicial .
A equação diferencial que modela o circuito RC é:
Deseja-se obter a resposta para , por meio do SIMULINK.
Passo 1
O exercício pede encontrarmos solucionado a EDO que modela o curcuito RC usando o SIMULINK. Uma dica para resolver uma EDO pelo SIMULINK é deixar a derivada isolada no lado esquerdo da equação. Por isso, vamos rearranjar a EDO para:
Com isso, identificamos a expressão que é igual à derivada, montamos o diagrama de blocos que a representa e, na saída desse diagrama, incluímos um bloco “Integrator” para ter . Este será conduzido a um bloco “Scope”, para vermos seu gráfico.
Passo 2
Sabendo que , e , a EDO se torna:
Logo, é igual a . Vamos começar modelando essa diferença. Em um novo modelo, insira um bloco “Constant” e faça com que ele seja igual a . Em seguida, insira um bloco “Add” e altere o parâmetro “List of signs” (destacado abaixo) para , de forma que “Add” tenha uma entrada positiva e outra negativa. Conecte “Constant” à entrada positiva:

Passo 3
A saída de “Add” será igual a , que é igual a . Por isso, colocaremos à direita de “Add” um bloco “Integrator”, para obter . Para isto, vá à biblioteca “Continuous”, insira um bloco “Integrator” ao modelo e conecte sua entrada à saída de “Add”, como na figura abaixo:
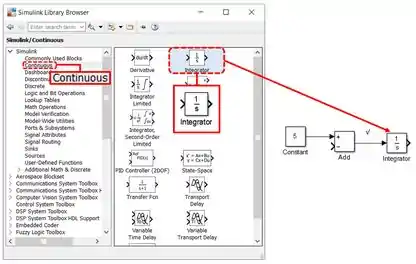
Precisamos mudar a condição inicial para . Acesse as propriedades de “Integrator” e altere o parâmetro “Initial Condition” de para :

Passo 4
A saída de “Integrator” será , a solução pedida pelo enunciado. Para gerar o gráfico dela, insira um bloco “Scope” e conecte a saída de “Integrator” à entrada de “Scope”:
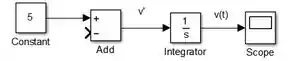
Leve para a entrada negativa de “Add”, para concluir a diferença . Para isto, clique sobre a entrada negativa de “Add” e arraste. Aparecerá uma flecha vermelha tracejada, cuja extremidade livre você deve conectar à seta entre “Integrator” e “Scope”:
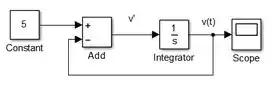
Pronto! Já montamos o diagrama de blocos que nos dará . Paa ver a curva de , execute o programa e clique duas vezes sobre o bloco “Scope”.
Resposta
