Considere o sistema massa-mola abaixo:
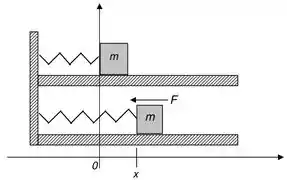
A posição do bloco de massa é representada por , sua velocidade por e sua aceleração por . As equações de movimento da Física nos dizem que e , onde é o tempo.
Pela 2ª lei de Newton, temos que a aceleração do bloco é dada por:
Onde é a rigidez da mola e é igual a .
A energia potencial do sistema é dada por:
E a energia cinética :
Considerando que o bloco parte do repouso, de uma posição inicial , utilize o SIMULINK para:
- Encontrar a solução de , para o intervalo de tempo ;
- Gerar os gráficos da energia potencial e da energia cinética.
Passo 1
Neste exercício, resolveremos uma EDO de segunda ordem, correspondendo à equação que calcula a aceleração pela 2ª lei de Newton. Substituindo e na EDO, temos:
Na letra do exercício, resolveremos a EDO acima, que nos dará , cujo gráfico iremos plotar usando um bloco “Scope”.
A partir do diagrama construído para resolver a letra , faremos a letra , pois o diagrama nos permitirá calcular as energias potencial e cinética do sistema. Ambas as energias também serão plotadas usando um bloco “Scope”.
Passo 2
Vamos começar a solucionar a EDO de segunda ordem. O enunciado no disse que e , logo:
Com essas informações podemos construir um diagrama inicial, inserindo em um novo modelo dois blocos “Integrator” e um bloco “Scope”, da seguinte forma:
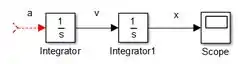
O primeiro “Integrator” receberá um sinal representando a aceleração , fará sua integração e nos dará a velocidade . entrará em um segundo bloco “Integrator” para obtermos , que é conduzido a um bloco “Scope” para plotarmos seu gráfico mais pra frente.
O enunciado diz que o bloco parte do repouso, indicando que a velocidade inicial é . Por isso, não precisamos alterar o parâmetro “Initial condition” do “Integrator” que recebe , pois o padrão do bloco “Integrator” é ter condição inicial nula.
Contudo, este não é o caso do segundo “Integrator”, que recebe o sinal de velocidade . O enunciado diz que o bloco parte da posição , por isso, temos que alterar o parâmetro “Initial condition” do “Integrator” que integra a velocidade e nos dá a posição (destacado abaixo):
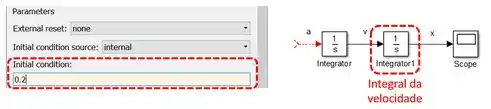
Passo 3
Com esse diagrama inicial, podemos partir para a EDO de segunda ordem para obtermos a aceleração . Insira no modelo um bloco “Gain” e altere seu ganho para :
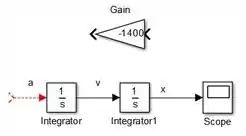
Queremos criar o termo , por isso, conecte a entrada de “Gain” à seta entre “Integrator1” e “Scope”:
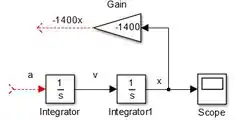
A saída de “Gain” será . E quam é igual a ? A aceleração ! Por isso, conecte a saída de “Gain” à entrada do primeiro “Integrator”, que ainda está vazia:
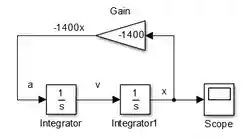
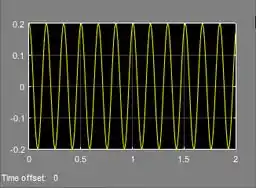
O diagrama que nos dá a solução da letra a do exercício está pronto! Com ele, podemos obter o gráfico de , que é a solução de . Para isto, altere o tempo de simulação de para , rode o programa e clique duas vezes sobre o “Scope” para ver o gráfico:
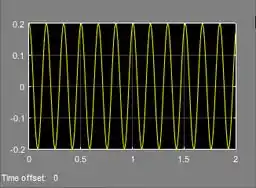
Pronto, letra a resolvida =)
Passo 4
A letra b do exercício pede para gerarmos os gráficos das energias potencial e cinética. A energia potencial é dada por , com . Logo, . Para obtermos a partir do diagrama construído para resolver a letra , vamos começar obtendo Para isto, usaremos o bloco “Product”, da biblioteca “Math Operations”, e faremos com que o sinal de entre em suas duas entradas:

Para calcular , insira um bloco “Gain”, faça-o ter um ganho igual a e conecte sua entrada à saída de “Product”:

A saída do bloco “Gain1” será a energia potencial .
Passo 5
A energia cinética é dada por , com . Logo, . Para obtermos a partir do diagrama construído para resolver a letra , vamos começar obtendo Para isto, usaremos outro bloco “Product”, que receberá o sinal de em suas duas entradas:
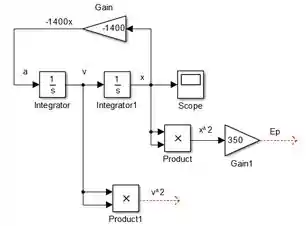
Para calcular , insira outro bloco “Gain”, faça-o ter um ganho igual a e conecte sua entrada à saída de “Product1”:

A saída do bloco “Gain2” será a energia cinética .
Vamos plotar as curvas de e no mesmo gráfico, conectando as duas saídas que dão de e a cada uma das entradas de um bloco “Mux”. A saída de “Mux” se conectará a um bloco “Scope”:
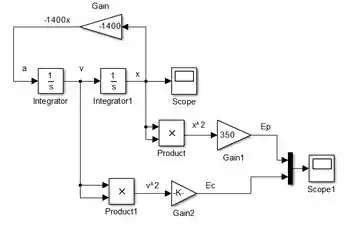
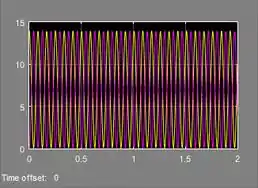
Como está conectado à entrada de cima de “Mux”, sua curva será amarela. Já a curva de será rosa, pois entra na entrada na de baixo de “Mux”.
Execute o programa e você terá o gráfico de ambas as energias.
Resposta
- A solução de é:
- A curva da energia potencial é a onda amarela e a curva da energia cinética é rosa.