Uma onda incide em uma superficíe quadrada. Sabendo que o módulo do campo elétrico dessa onda é , encontre a aresta do prisma representado abaixo e a intensidade da luz que emite essa onda, sabendo que a potência da fonte de luz é 2,39W.
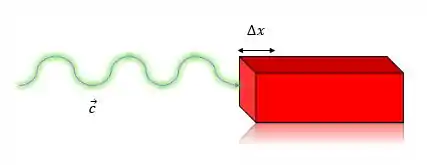
Passo 1
Precisamos encontrar a intensidade da fonte e a aresta, vamos começar com o volume que é dado por:
Onde é a área da seção transversal do prisma.
Podemos usar a densidade de energia elétrica para encontrarmos a densidade de energia total
já que temos o campo elétrico.
A densidade de energia total é inicialmente dada por:
Mas:
Se a densidade de energia é:
E a energia é:
A gente pode substituir e a fórmula vai ficar assim:
Passo 2
Com as duas equações da densidade, podemos igualá-las assim:
Relacionando potência e intensidade, conseguimos eliminar uma incógnita:
Voltando na equação, temos:
Mas:
Substituindo na equação e rearrumando, temos a intensidade:
Passo 3
Agora com a intensidade e a potência, a gente consegue encontrar a área de boa, lembrando que:
E como a área é quadrada, temos que: