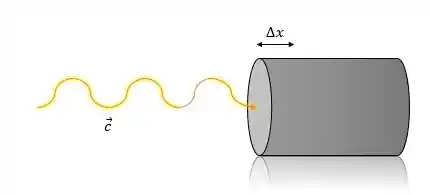
Prove as fórmulas das densidades de energia elétrica e magnética partindo da ideia mostrada na figura abaixo. A onda desloca o cilindro uma distância no sentido de propagação da mesma.
Passo 1
As densidades de energia são nada mais que energia por quantidade de volume. Observe que na figura, a onda desloca a distância a partir da face do cilindro. Assim, o volume que a energia preenche será:
Onde é a área da seção transversal do cilindro.
A densidade de energia é dada inicialmente por:
E a energia é:
Se a gente olhar a fórmula da intensidade, podemos relaciona-lá com a potência dessa forma:
A energia será então:
Passo 2
Vamos substituir o que encontramos na equação da densidade e ela vai ficar mais ou menos assim:
Como estamos trabalhando com uma onda eletromagnética, a velocidade é , então podemos dizer que:
Na equação temos o inverso disso, então o aparece embaixo e vai ficar assim:
Passo 3
Bom, a gente tem que chegar na densidade de energia magnética e agora só nos restou a intensidade pra mexer. Bora ver no que dá.
A fórmula da intensidade média diz que:
E se substituirmos na equação:
Vamos chegar nisso aqui:
Agora só precisamos usar a relação:
E a nossa equação vai ficar assim:
Passo 4
Para a densidade de energia elétrica, basta usarmos a relação:
E a densidade de energia magnética vai ficar:
Como:
Temos na equação: