Exercícios Resolvidos de Entalpia, Energia Interna e Calores Específicos de Gases Perfeitos
Ver TeoriaEnunciado
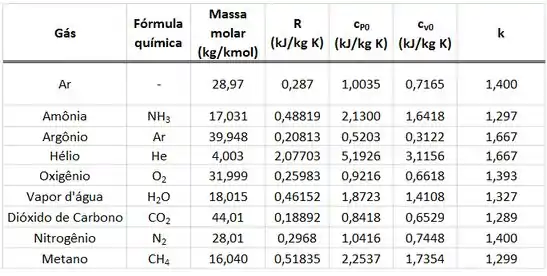
Determine a variação de energia interna específica para o quando este é aquecido de a utilizando:
- o valor de da Tab. A.5
- o valor de avaliado com a equação presente na Tab. A.6 e na temperatura média do intervalo.
- Os valores de apresentados na Tab. A.8
Passo 1
Fala, galera! Vamos fazer esse exercício para entender como se usa o calor específico a volume constante no cálculo da variação de energia interna específica ?
O exercício quer que a gente calcule a variação de energia interna , quando o aumenta sua temperatura de até ! Pra achar de um gás perfeito através de , usamos sempre a integral abaixo.
A questão quer que a gente ache o valor de , usando dois valores de diferentes obtidos nas duas tabelas (Tab. A.5 e Tab. A.6) e usando os valores de entalpia da Tab. A.8.
Primeiro, a questão quer que a gente ache , considerando o valor de constante e igual ao valor presente na tabela A.5. Sabendo disso, já podemos achar no próximo passo!
Passo 2
O primeiro jeito de encontrar o valor de é achar o valor de na tabela abaixo e substituir esse valor na integral do passo 1.
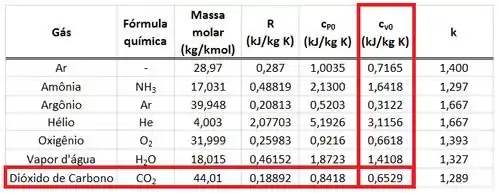
Através dessa tabela, vemos que o calor específico a volume constante do vale:
Substituindo esse valor na integral ela vira:
Colocando a constante pra fora da integral e integrando , achamos:
Aeeee! A letra (a) da questão já foi resolvida. Agora vamos encontrar da segunda forma!
Passo 3
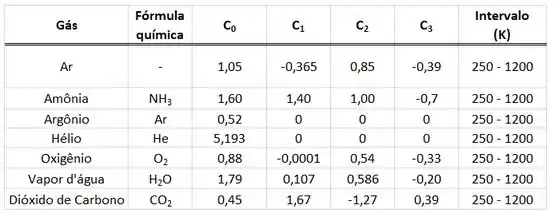
Para encontrar da segunda forma, temos que achar o valor de através da equação de fornecida pela tabela A.6. Essa fórmula nos dá os valores de para qualquer valor da temperatura do gás. Como o valor da temperatura de varia de a , o enunciado pede para a gente usar o calor específico da temperatura média na integral.
Para achar a partir do da tabela, usamos a equação de gases perfeitos abaixo.
onde é a constante de gás do e é encontrada na tabela anterior. Ela vale .
é calculado através da equação abaixo.
onde é a temperatura que usamos pra calcular dividida por . Logo, é:
No próximo passo acharemos , , e através da tabela A.6, para achar da segunda forma.
Passo 4
Os coeficientes , , e estão presentes na tabela abaixo.
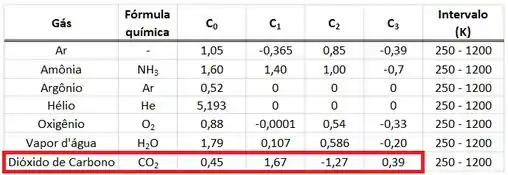
Substituindo esses valores na equação de :
Usando a equação que calcula a partir de :
Para encontrar , substituímos esse valor de na integral do passo 1, colocamos a constante pra fora e integramos .
Resolvemos a letra (b)! Então vamos tentar resolver a letra (c), calculando da terceira forma!
Passo 5
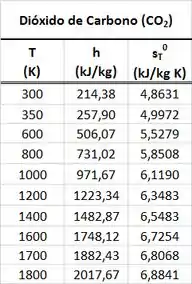
Pra calcular a variação de energia interna da terceira forma, temos que encontrar o valor da energia interna que o tinha e o valor de energia interna que o passou a ter depois de aumentar sua temperatura.
Pra encontrar e , usamos os valores da entalpia que o tinha quando sua temperatura media e da entalpia que o passou a ter quando sua temperatura passou a medir . e estão presentes na tabela abaixo.
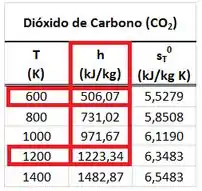
Pra encontrar e a partir de e , usamos as fórmulas que servem apenas para gases perfeitos encontradas abaixo:
Substituindo os dados que temos:
Com e somos, enfim, capazes de achar :
Com a resposta da letra (c) encerramos esse exercício! Ele te ajudou a fixar o conteúdo da teoria? Responde aí!