Exercícios Resolvidos de Entalpia, Energia Interna e Calores Específicos de Gases Perfeitos
Ver TeoriaEnunciado
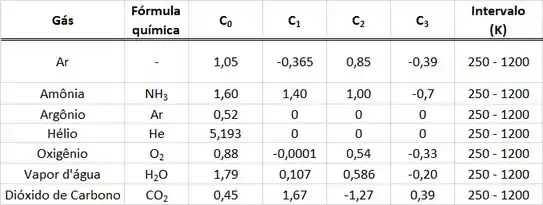
Um tanque rígido contendo de dióxido de carbono recebe de calor. Utilizando um polinômio para calcular o calor específico do determine a variação da temperatura do com esse processo. Suponha que o calor específico do é constante e é igual ao calor específico avaliado na temperatura de . Utilize as tabelas abaixo.
Passo 1
Tudo tranquilo, gente? Vamos direto ao ponto e descobrir como usar o calor específico de um gás perfeito pra calcular a variação de temperatura do gás?
Esse exercício quer saber quanto vale a variação de temperatura do , quando ele recebe de calor! A figura abaixo mostra os dados que temos pra calcular .
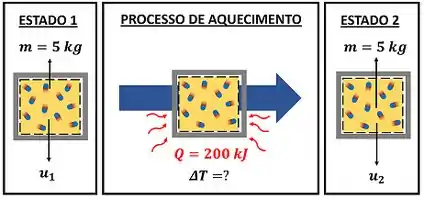
é a energia interna do antes de ser aquecido e é a energia interna do depois de ser aquecido. é o calor trocado entre o ar e o ambiente.
O primeiro passo pra achar , é aplicar a primeira lei no tanque rígido.
Para usar essa equação, precisamos lembrar que o trabalho vale zero, porque o tanque não permite a variação de volume do gás.
Usando a primeira lei, somos capazes de achar a variação de energia interna . Conhecer quanto vale é fundamental pra achar . A equação de gases ideais abaixo mostra a relação entre e pra gases com calor específico constante.
onde é o calor específico a volume constante do que será encontrada a partir da equação presente em uma tabela.
Com todas essas informações em mãos, estamos aptos a achar no próximo passo.
Passo 2
A primeira etapa passo pra calcular é achar , reorganizando a primeira lei da termodinâmica.
Agora só falta achar pra calcular .
Passo 3
Para achar o valor de , temos que usar a equação de fornecida por uma tabela. Essa fórmula nos dá os valores de para qualquer valor da temperatura do gás. O enunciado pede para a gente usar o calor específico da temperatura de .
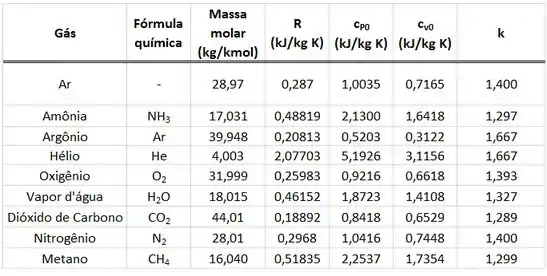
Para achar a partir do da tabela, usamos a equação de gases perfeitos abaixo.
onde é a constante de gás do que vale .
é calculado através da equação abaixo.
onde é a temperatura que usamos pra calcular dividida por . Logo, é:
Os coeficientes , , e estão presentes na tabela abaixo.
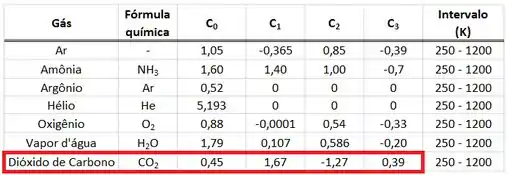
Substituindo esses valores na equação de :
Usando a equação que calcula a partir de :
Agora estamos aptos a achar !
Passo 4
Substituindo os valores de e , na fórmula de :
Que ótimo! Já achamos o resultado que o enunciado pediu!