Exercícios Resolvidos de Entalpia, Energia Interna e Calores Específicos de Gases Perfeitos
Ver TeoriaEnunciado
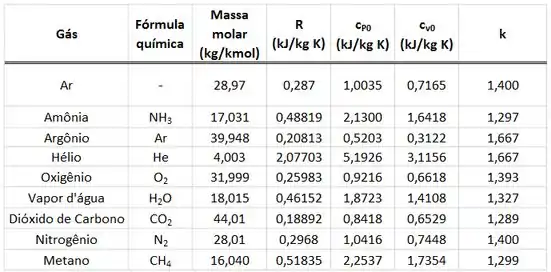
Um tanque rígido com volume interno igual a contém gás metano a e . O tanque é, então, resfriado até . Determine a massa de metano contida no tanque e o calor transferido no processo utilizando as tabelas de gás perfeito. Use a tabela abaixo.
Passo 1
Oi, gente! Esse é um exercício que pede pra gente calcular a massa de metano contida no tanque e o calor trocado entre metano do tanque e o ambiente.
Para calcular o calor trocado entre o tanque e o ambiente durante o processo que resfria o metano da temperatura até a temperatura , usamos a primeira lei.
onde é a energia interna do metano depois de ser resfriado a e é a energia interna do metano a e pressão . é o trabalho de movimento de fronteira que o metano realiza sobre o ambiente. Como o tanque é rígido, não tem como o metano mudar seu volume e movimentar suas fronteiras. Logo, o trabalho vale zero!
Pela fórmula de , vemos que precisamos achar a massa de metano primeiro, pra encontrar depois. Achamos essa massa , aplicando a equação dos gases perfeitos no metano que ainda não foi resfriado.
onde é a constante de gás do metano que vale e é o volume do tanque que vale .
Como já temos todos os dados necessários, vamos calcular a massa de metano no próximo passo.
Passo 2
Antes de usar a fórmula de , precisamos converter o volume de pra , dividindo por !
Substituindo esse valor na fórmula de :
Pronto, já achamos uma informação que o enunciado pediu.
Agora, só precisamos aprender a calcular a diferença de energia interna pra conseguir calcular o calor . Faremos isso no próximo passo!
Passo 3
Pra achar a diferença entre energias internas , podemos usar a fórmula de diferença de energia interna dos gases perfeitos com calor específico constante.
onde é o calor específico a volume constante do metano que vale segundo a tabela de gases perfeitos abaixo.
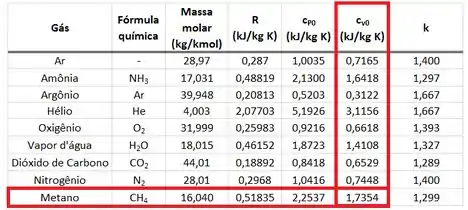
Substituindo , e na equação de , encontramos:
Usando esse valor, podemos achar quanto vale .
Aeeeee! Achamos o calor trocado que a questão pedia pra gente! Acabamos com esse exercício!