Exercícios Resolvidos de Entalpia, Energia Interna e Calores Específicos de Gases Perfeitos
Ver TeoriaEnunciado
Inicialmente, a água de uma amostra se encontra a e . A água é então aquecida até que o estado onde a temperatura e a pressão são iguais a e . Determine a variação de energia interna no processo utilizando as tabelas de propriedades termodinâmicas da água e as tabelas de gás perfeito.
Passo 1
Oi, gente, partiu fazer esse exercício de cálculo de variação de energia interna específica da água?
Esse exercício quer saber o da água, quando água líquida a e com energia interna específica é aquecida até virar um vapor muito superaquecido (também chamado de gás) a , e energia interna específica .
Como a água que tem energia interna é líquida, não devemos usar as tabelas de gás perfeito pra achar . Achamos através das tabelas de propriedades termodinâmicas! No entanto, não podemos usar essa tabela pra achar , porque a temperatura é maior que a temperatura de vapor presente na tabela. No próximo passo resolveremos isso!
Passo 2
Já sabemos onde encontrar , mas como achamos a energia interna específica do vapor superaquecido a , se não existe informações do vapor a essa temperatura na tabela de propriedades da água?
Pra contornar esse problema, temos que dividir o cálculo de no cálculo de e .
é a variação de energia interna que a água tem, quando vai de , e a , e . é a energia interna do vapor que conseguimos obter através da tabela da água! Ou seja, é a variação de energia interna da água que a gente consegue calcular usando apenas as tabelas de propriedades da água.
é a variação de energia interna da água que podemos calcular usando apenas a tabela de gás perfeito de . Ou seja, é a variação da energia interna do gás perfeito de água, quando ele vai de e a e . é a energia interna específica do gás obtida na tabela de gás perfeito. Por isso, é diferente de .
No próximo passo nós vamos achar e na tabela termodinâmica da água e calcular !
Passo 3
Primeiro, encontramos a energia interna da água líquida comprimida a e . Como não tem tabela pra água líquida comprimida a essa pressão e temperatura, usaremos a energia interna da água líquida saturada a obtida da tabela abaixo.
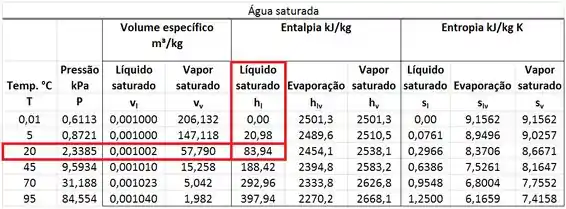
é um vapor superaquecido a e . Logo, achamos a partir da tabela de vapor superaquecido nessa temperatura e pressão.
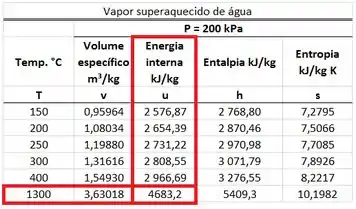
Substituindo e na equação de , achamos:
Boa! Calculamos a primeira parte de . Então vamos partir para o cálculo de no próximo passo para conseguir calcular !
Passo 4
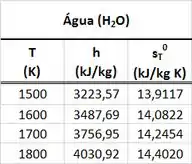
Pra calcular , temos que encontrar o valor das energias internas e usamos os valores da entalpia de a e da entalpia de a presentes na tabela de gás perfeito de . Para achar e , temos primeiro que converter as unidades das temperaturas e de pra .
Não conseguimos encontrar os valores de entalpia pra essas temperaturas através da tabela de gases perfeitos que temos. Por isso, teremos que interpolar os valores de entalpia!
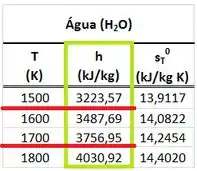
Pra encontrar e a partir de e , usamos as fórmulas que servem apenas para gases perfeitos encontradas abaixo:
onde é a constante de gás da água que vale .
Substituindo os dados que temos:
Com e somos, enfim, capazes de achar :
Somando com , achamos !
Aeeee! Foi sofrido, mas achamos o que o enunciado pediu! Pra isso, tivemos que dividir o em uma parcela que era encontrada nas tabelas de propriedades e em outra parcela que era obtida nas tabelas de gases perfeitos. mas apesar do trabalho deu tudo certo! :)