Exercícios Resolvidos de Entalpia, Energia Interna e Calores Específicos de Gases Perfeitos
Ver TeoriaEnunciado
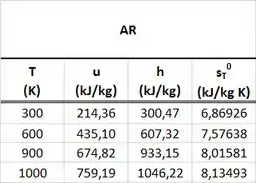
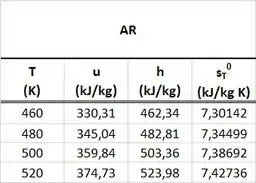
Um tanque rígido e isolado termicamente está dividido em duas regiões por meio de uma membrana (veja o esboço da Fig. P5.58). A região apresenta e contém ar a e . A região apresenta e contém ar a e . A membrana é, então, rompida e espera-se que seja estabelecido o equilíbrio. Determine a pressão e a temperatura do ar no estado final deste processo. Use as tabelas abaixo.
Passo 1
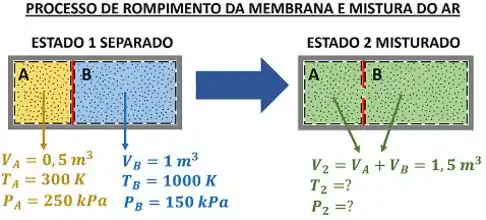
E aí, querid@s! Indo direto ao ponto, esse exercício quer saber quanto valem a pressão e a temperatura do ar, depois da membrana furar e permitir que o ar das regiões e se misturem. A figura abaixo mostra os dados que temos pra calcular e .
Como o tanque com ar está isolado termicamente, a troca de calor entre o ar e o ambiente vale zero.
Além disso, o trabalho realizado pela ar no ambiente vale zero, porque a mistura de ar é apenas uma expansão não resistida.
Essas duas informações são muito importantes! Usando esses novos dados na equação de conservação de energia, descobrimos quanto vale a energia interna específica do ar misturado! Saber quanto vale é fundamental pra achar a temperatura do ar misturado (que é uma incógnita do problema) através da tabela de gases perfeitos.
onde é a energia interna do ar misturado e é a soma da energia interna da região com a energia intern da região .
No entanto, a energia interna é sempre a massa multiplicada pela energia interna por unidade de massa .
Agora que temos uma fórmula pra achar , podemos começar a encontrar as variáveis , , , e que são necessárias para acharmos . No próximo passo a gente vai iniciar as contas, encontrando , e .
Passo 2
Para achar a massa de ar da região , usamos a equação de gases perfeitos abaixo.
onde é a constante de gás do ar que vale .
Substituindo esse valor na fórmula de :
Também temos que usar a equação de gases perfeitos pra descobrir a massa da região .
A massa de ar misturado é a soma das massas e que o ar tinha antes de se misturar.
Agora só falta encontrar e através das tabelas de gás perfetio na próxima etapa pra poder achar .
Passo 3
Para achar e , vamos precisar usar a tabela de gás perfeito do ar abaixo.
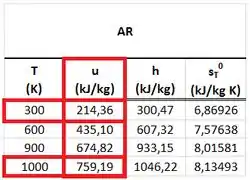
Substituindo esss dois valores na fórmula de :
Como vocês podem ver pela tabela de gás perfeito do ar abaixo, a energia interna é correspondente a uma temperatura que está entre e . Logo, faremos uma interpolação pra achar a temperatura através dessa tabela.
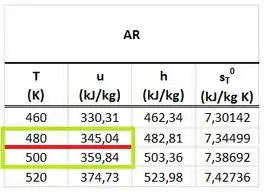
Que beleza! Encontramos uma das informações que o enunciado pedir! Agora só falta encontrar no próximo passo!
Passo 4
Para encontrar a pressão do ar misturado, usaremos a equação de gás perfeito para o ar misturado.
Pronto, achamos a pressão e fechamos o exercício! Uhuuuul!