Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Escoamento sob comporta e ressalto hidráulico

Ver Teoria
Exercício 61234578

Enunciado

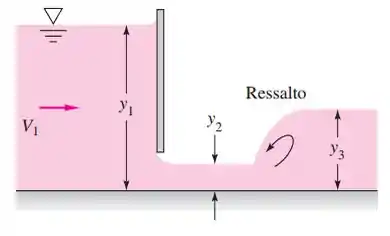
Para a situação na Figura, considere que na seção 3 a profundidade seja de 2 m e que o número de Froude seja 0,25. Calcule (a) a vazão por metro de largura, (b) y c , (c)     y 1 , (d) o percentual de dissipação no ressalto hidráulico e (e) a altura da abertura H da comporta.

Passo 1

Então time, vamos relacionar os dois temas que vimos nesse tópico: comportas e o ressalto hidráulico.

As coisas são mais conta que difíceis. Vamos calcular as propriedades da cada seção 3,2 , 1 nesta ordem, pois temos valores no enunciado da etapa 3 .

Deveremos então analisar o balanço energético depois do ressalto e ir retornando, fazendo as transições corretas.

Passo 2

Vamos começar calculando a velocidade V 3 a partir de F r 3 e y 3 , para encontramos q :

V 3 = F r 3 g y 3

V 3 = 0,25 * 9,81 * 2

V 3 = 1,11 m s

Lembrando que q = V y :

q = 1,11 * 2

q = 2,22 m s . m

Passo 3

Para calcularmos a profundidade crítica devemos lembrar do tópico anterior:

y c = q 2 g 1 / 3

y c = 2,22 2 9,81 1 / 3

y c = 0,79   m

Passo 4

Para encontrarmos y 1 devemos conhecer as propriedades em 2 , aplciaremos então a teoria de ressaltos hidráulicos:

y 2 y 3 = - 1 + 1 + 8 F r 2 2 2

Esta expressão pode ser reescrita para o caminho contrário, ou seja, calcular de 3 → 2 , ao invés de 2 → 3 :

y 2 y 3 = - 1 + 1 + 8 F r 3 2 2

Substituindo os valores conhecidos:

y 2 2 = - 1 + 1 + 8 ( 0,25 ) 2 2

y 2 = 0,22   m

Calculamos V 2 = q y 2 :

V 2 = 2,22 0,22 = 10,1 m s

Calcularemos a energia em 2 , que é a mesma que em 1 pois não temos elevação:

E 2 = y 2 + V 2 2 2 g = y 1 + V 1 2 2 g

y 1 + V 1 2 2 g = 0,22 + 10,1 2 2 * 9,81

y 1 + V 1 2 2 g = 5,42   m

Lembramos também da equação da continuidade:

q = V 1 y 1

V 1 = q y 1

Substituindo uma na outra:

y 1 + q 2 2 g y 1 2 = 5,42

y 1 + 2,22 2 2 * 9,81 * y 1 2 = 5,42

y 1 + 0,25 y 1 2 = 5,42

Multiplicando ambos lados por y 1 2 : y 1 3 + 0,25 = 5,42 y 1 2

Temos uma equação de terceiro grau, com uma única solução positiva:

y 1 = 5,41   m

É um resultado aproximado da solução da equação.

Passo 5

A dissipação no ressalto é

h p = y 3 - y 2 3 4 y 2 y 3

h p = 2 - 0,22 3 4 * 2 * 0,22

h p = 3,2   m

Sabemos que a energia em 2 é:

E 2 = 5,42   m

Logo o percentual de perda é:

3,2 5,42 = 59 %

Passo 6

E finalmente para calcularmos a abertura H da comporta:

Q = C d H b 2 g y 1

C d = 0,61 1 + 0,61 H y 1

Substituiremos C d na expressão de Q e substituiremos Q b = q :

q = 0,61 1 + 0,61 H y 1 H 2 g y 1

q 1 + 0,61 H y 1 = 0,61 H 2 g y 1

Elevando ambos lados ao quadrado:

q ² 1 + 0,61 H y 1 = 0,61 H ² * 2 g y 1

0,7442 H ² g y 1 q ² - 0,61 H y 1 - 1 = 0

Substituido os valores conhecidos:

H 2 0,7442 * 9,81 * 5,41 2,22 2 - H 0,61 5,41 - 1 = 0

8 H 2 - 0,11 H - 1 = 0

Resolvendo a equação de segundo grau:

H = 0,36   m

Esta é a única raiz positiva.

Resposta

a   q = 2,22 m s . m

b   y c = 0,79   m

c   y 1 = 5,41   m

d   59 %

e   H = 0,36   m

Exercícios de Livros Relacionados

Um ressalto hidráulico ocorre em um largo canal horizontal. A descarga é de 2m 3 / s por m de largura. A profundidade a montante é de 750m m . Determine a profundidade do ressalto.
Um canal largo carrega 10m 3 / s por m de largura a uma profundidade de 1m no pé de um ressalto hidráulico. Determine a profundidade do ressalto e perda de carga através desse.
Determine a taxa na qual a energia está sendo consumida ( k W ) pelo ressalto hidráulico do Exemplo 11.5. Essa taxa é suficiente para produzir um significativo aumento de temperatura na água?
Um ressalto hidráulico ocorre em um canal retangular com 4,0m de largura. A profundidade da água antes do ressalto é de 0,4m , e de 1,7m após o ressalto. Calcule a vazão no canal, a profundidade críti
Um ressalto hidráulico ocorre sobre um anteparo horizontal a jusante de um largo vertedouro, em um local onde a profundidade é igual a 0,9 m e a velocidade é igual a 25m / s . Estime a profundidade e