Probabilidade Total e Teorema de Bayes
b) Defina formalmente uma partição de um espaço amostral. Use o diagrama de Venn para ilustrar.
Passo 1
Vamos supor um espaço amostral, .
Vamos dizer também que temos vários eventos: .
Dizemos que esses eventos formam uma partição do nosso espaço amostral, se:
- Todos tiverem probabilidade de acontecer maior que 0:
- Eles forem mutuamente exclusivos, ou seja, a interseção de qualquer um deles ser nula:
- A união de todos eles formar o nosso espaço amostral:
Passo 2
Usando o diagrama, teríamos algo assim:
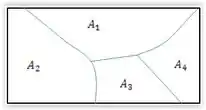
Em poucas palavras, partição de um espaço amostral, são vários eventos mutuamente exclusivos cuja união forma o espaço amostral.
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
(l) Mesmo enunciado que (j), sem reposição.
Forneça uma descrição razoável do espaço amostral para cada uma das experiências aleatórias nos Exercícios 2-1 a 2-18. Poderá haver mais de uma interpretação aceitável para cada experimento.Descreva q
Forneça uma descrição razoável do espaço amostral para cada uma das experiências aleatórias nos Exercícios 2-1 a 2-18. Poderá haver mais de uma interpretação aceitável para cada experimento.Descreva q
Forneça uma descrição razoável do espaço amostral para cada uma das experiências aleatórias nos Exercícios 2-1 a 2-18. Poderá haver mais de uma interpretação aceitável para cada experimento.Descreva q
Forneça uma descrição razoável do espaço amostral para cada uma das experiências aleatórias nos Exercícios 2-1 a 2-18. Poderá haver mais de uma interpretação aceitável para cada experimento.Descreva q