Escrever a Tag aqui (nome do capítulo IGUALZINHO), Outra tag, Mais uma tag
Um espelho côncavo forma uma imagem real, que tem o dobro do tamanho do objeto. Se o objeto está a uma distância de 20 cm do espelho, o raio de curvatura do espelho é de cerca de:
Passo 1
No espelho côncavo, as características da imagem formada dependem da distância do objeto até o espelho. Imagina o objeto à esquerda do espelho.
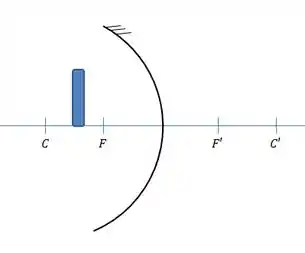
Para a imagem formada ser real, ela deve também ser formada à esquerda do espelho (a imagem é dita “real” quando ela é formada pelos próprios raios de luz).
Se o objeto estiver entre o foco e o espelho, a imagem formada é virtual, logo não é o nosso caso.
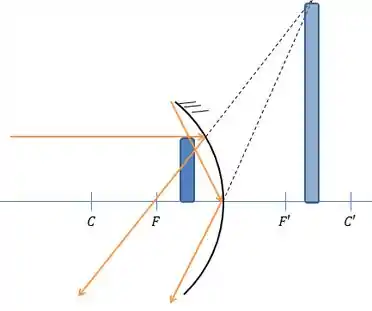
A medida que o objeto vai se aproximando do foco, os dois prolongamentos vão se encontrando cada vez mais longe até que, quando o objeto está no foco, os prolongamentos só encontrariam no infinito (ou seja, não forma imagem).
Assim, temos certeza que o objeto está antes do foco. Nestes casos, temos:
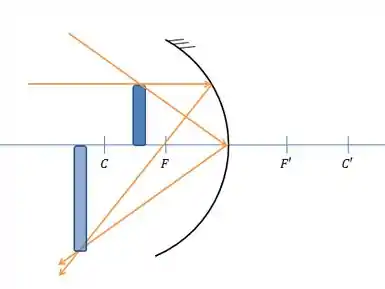
Ou seja, a imagem passa a ser real e invertida. A medida que vamos afastando o objeto do espelho, o raio que incide no centro do espelho vai formando ângulos mais fechados, e a imagem vai andando para a direta e diminuindo cada vez mais.
Passo 2
Agora, vamos fazer uma segunda observação: A imagem só é maior que o objeto quando o objeto está entre o centro de curvatura e o foco.
Quando o objeto está exatamente no centro de curvatura, a imagem também vai estar. Pela equação para espelhos esféricos:
No centro de curvatura, . Logo:
Neste caso, o objeto e a imagem terão exatamente o mesmo tamanho, pois a ampliação vai ser:
Onde o sinal mostra apenas que a imagem é invertida. Com isso, temos certeza que o objeto está entre o foco e o centro de curvatura. Agora o próximo passo é encontrar este centro de curvatura.
Passo 3
Já temos o problema todo visualizado. Agora é fazer conta.
Se a imagem tem o dobro do tamanho do objeto, temos que a ampliação vai ser , visto que:
Onde é o tamanho da imagem e é o tamanho do objeto, e a imagem é invertida. Substituindo na fórmula para a ampliação:
Como pelo enunciado o objeto está a uma distância de do espelho, a imagem estará a uma distância de do espelho. Substituindo na equação dos espelhos esféricos:
A distância do centro de curvatura até o espelho é duas vezes maior que à do foco.
Alternativa de “centro de curvatura”.
Resposta
Alternativa .