A figura abaixo mostra a ampliação lateral de um objeto em função da distância do objeto em relação a um espelho esférico quando o objeto é deslocado ao longo do eixo central do espelho.
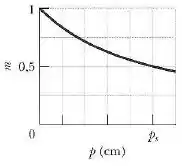
A escala do eixo horizontal é definida por . Qual é a ampliação do objeto quando este se encontra a do espelho?
Passo 1
Vamos começar calculando a distância focal da lente.
Para isso, um bom ponto no gráfico para começarmos a trabalhar é o ponto cujas coordenadas são:
Logo:
Passo 2
A distância focal será:
Substituindo os valores, teremos:
Passo 3
A distância quando será:
Passo 4
A ampliação lateral desejada será dada por:
Resposta
Exercícios de Livros Relacionados
Uma moeda é isolada ao lado convexo de um concha de vidro delgada e esférica com um raio de curvatura de 18,0 cm. Uma imagem da moeda de 1,5 cm de altura é formada há 6,0 cm da concha de vidro. Onde a
Espelhos esféricos. Um objeto O está sob o eixo central de um espelho esférico. Para cada problema a tabela mostra a distância do objeto p (em centímetros), o tipo de espelho e a distância (em centíme
Um objeto é colocado no centro de um espelho esférico e deslocado ao longo do eixo central até uma distância de 70c m do espelho. Durante o movimento, a distância i entre o espelho e a imagem do objet
Estime a distância focal do “espelho” produzido pela superfície da água de uma piscina em uma noite calma.