Materiais funcionalmente graduados são intencionalmente fabricados para estabelecerem uma distribuição espacial de propriedades no produto final. Seja um objeto L × L bidimensional, com L = 20 mm. A distribuição de condutividades térmicas no material funcionalmente graduado é . Dois conjuntos de condições de contorno, identificados por casos 1 e 2, são aplicados.
- Determine o valor médio espacial da condutividade térmica . Use este valor para estimar a taxa de transferência de calor por unidade de comprimento nos casos 1 e 2.
- Usando um espaçamento na grade de 2 mm, determine a taxa de transferência de calor por unidade de comprimento no caso 1. Compare o seu resultado com o valor estimado calculado na parte (a).
- Usando um espaçamento na grade de 2 mm, determine a taxa de transferência de calor por unidade de comprimento no caso 2. Compare o seu resultado com o valor estimado calculado na parte (a).
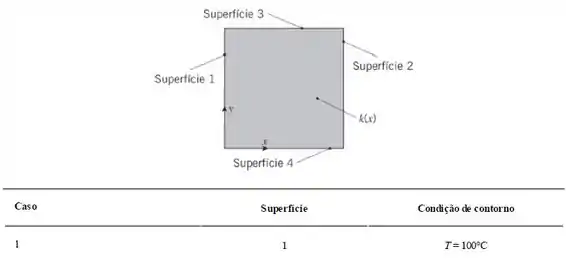

Passo 1
Boom galerinha, na letra (a) nós queremos achar o valor médio espacial da condutividade térmica e, com ela, estimar a taxa de transferência de calor por unidade de comprimento nos casos 1 e 2.
Bora começar?
A condutividade térmica média é dada por:
Se:
Então:
Aplicando o intervalo:
Substituindo o L:
E a transferência de calor trocado entre as superfícies 1 e 2 ou 3 e 4:
Como queremos por unidade de comprimento:
Substituindo:
Ou melhor:
Passo 2
Na letra (b) nós vamos desenhar o espaçamento na grade de 2 mm, deem uma olhadinha:
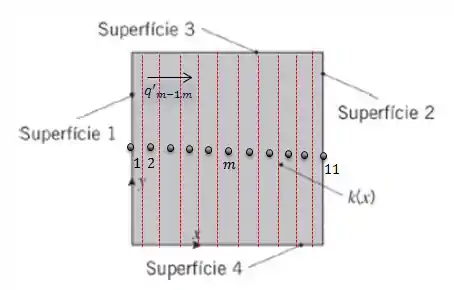
Como a transferência de calor é unidimensional e vai da superfície 1 para a 2 (caso 1) ou da superfície 4 para a 3 (caso 2) nós podemos começar calculando o k para divisão entre as superfícies:
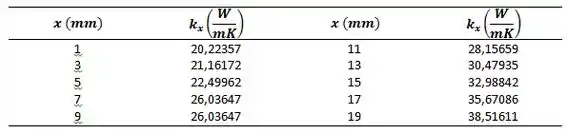
Se assumimos que o estado é estacionário, a transferência de calor por unidade de comprimento é constante!!
Se é assim, cada linhazinha terá a mesma transferência por condução e se chamarmos .
Para o primeiro intervalo:
Fazendo isso para todas as linhas e somando todos os intervalos para alcançar :
Substituindo os valores da Tabela acima:
Para os dez espaçamentos:
Passo 3
No caso 2 nós teremos o fluxo de calor na direção vertical nós teremos:
Para as 10 linhas que nós temos:
Multiplicando pelo valor total:
Substituindo:
O que vocês acharam desta, ein ?!