Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 4.Problemas - Ex. 38

Seja a configuração nodal 2 da tabela 4.2 . Deduza as equações de diferenças finitas, para condições de regime estacionário, nas seguintes situações.

(a) O contorno horizontal do vértice interno está perfeitamente isolado e o contorno vertical sujeito a um processo de convecção ( T ∞ , h ) .

(b) Os contornos do vértice interno estão perfeitamente isolados. Como esse resultado se compara com a equação 4.41 ?

Passo 1

A configuração nodal 2 é

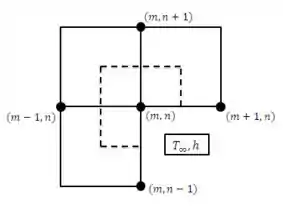
Desenhando as taxas de transferência de calor no volume de controle:

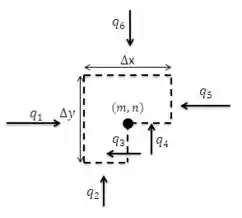
Antes de deduzir a equação de diferenças finitas vamos ressaltar que o contorno horizontal do vértice está isolado, então q 4 = 0 .

Para deduzir vamos começar com o balanço de energia para regime estacionário:

d E d t = E ˙ e n t - E ˙ s a í d a

0 = E ˙ e n t

0 = q 1 + q 2 + q 3 + q 5 + q 6

Passo 2

Vamos agora calcular separadamente cada uma das taxas de transferência de calor. Começando com q 1 :

q 1 = q ( m - 1 , n ) → ( m , n )

q 1 = k A L ∆ T

q 1 = k ∆ y ∙ 1 ∆ x T m - 1 , n - T m , n

Para q 2 :

q 2 = q ( m , n - 1 ) → ( m , n )

q 2 = k A L ∆ T

q 2 = k ∆ x 2 ∙ 1 ∆ y T m , n - 1 - T m , n

Vamos agora para a transferência de calor por convecção q 3 :

q 3 = q c o n v , x

q 3 = h A ∆ T

q 3 = h ∆ y 2 ∙ 1 T ∞ - T m , n

A relação para q 5 é:

q 5 = q ( m + 1 , n ) → ( m , n )

q 5 = k A L ∆ T

q 5 = k ∆ y 2 ∙ 1 ∆ x T m + 1 , n - T m , n

Finalmente, a equação de q 6 :

q 6 = q ( m , n + 1 ) → ( m , n )

q 6 = k A L ∆ T

q 6 = k ∆ x ∙ 1 ∆ y T m , n + 1 - T m , n

Passo 3

Voltando para o balanço de energia:

q 1 + q 2 + q 3 + q 5 + q 6 = 0

k ∆ y ∙ 1 ∆ x T m - 1 , n - T m , n + k ∆ x 2 ∙ 1 ∆ y T m , n - 1 - T m , n + h ∆ y 2 ∙ 1 T ∞ - T m , n + k ∆ y 2 ∙ 1 ∆ x T m + 1 , n - T m , n + k ∆ x ∙ 1 ∆ y T m , n + 1 - T m , n = 0

Para ∆ x = ∆ y :

k T m - 1 , n - T m , n + k 2 T m , n - 1 - T m , n + h ∆ y 2 T ∞ - T m , n + k 2 T m + 1 , n - T m , n + k T m , n + 1 - T m , n = 0

2 T m - 1 , n - T m , n + T m , n - 1 - T m , n + h ∆ y k T ∞ - T m , n + T m + 1 , n - T m , n + 2 T m , n + 1 - T m , n = 0

2 T m - 1 , n + T m , n + 1 + T m , n - 1 + T m + 1 , n + h ∆ y k T ∞ - 6 + h ∆ y k T m , n = 0

Passo 4

Vamos agora para o item (b). Neste item, ambos os contornos do vértice estão isolados. Então q 3 = 0 e q 4 = 0 . Se retirarmos o termo q 4 da equação ficaremos com:

q 1 + q 2 + q 5 + q 6 = 0

k ∆ y ∙ 1 ∆ x T m - 1 , n - T m , n + k ∆ x 2 ∙ 1 ∆ y T m , n - 1 - T m , n + k ∆ y 2 ∙ 1 ∆ x T m + 1 , n - T m , n + k ∆ x ∙ 1 ∆ y T m , n + 1 - T m , n = 0

Se fizermos ∆ x = ∆ y :

k T m - 1 , n - T m , n + k 2 T m , n - 1 - T m , n + k 2 T m + 1 , n - T m , n + k T m , n + 1 - T m , n = 0

2 T m - 1 , n - T m , n + T m , n - 1 - T m , n + T m + 1 , n - T m , n + 2 T m , n + 1 - T m , n = 0

2 T m - 1 , n + T m , n + 1 + T m , n - 1 + T m + 1 , n - 6 T m , n = 0

Comparando com a equação 4.41 podemos ver que essa relação é equivalente à situação em que a convecção não é considerada.

Resposta

(a) 2 T m - 1 , n + T m , n + 1 + T m , n - 1 + T m + 1 , n + h ∆ y k T ∞ - 6 + h ∆ y k T m , n = 0 .

(b) 2 T m - 1 , n + T m , n + 1 + T m , n - 1 + T m + 1 , n - 6 T m , n = 0 ; Comparando com a equação 4.41 podemos ver que essa relação é equivalente à situação em que a convecção não é considerada para a configuração nodal 2.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja o domínio bidimensional mostrado. Todas as superfícies estão isoladas a menos das superfícies isotérmicas em x = 0 e L. Use uma análise unidimensional para estimar o fator de forma S.Estime o fat
O fator de forma para a condução através do canto formado por duas paredes adjacentes, com D L 5 , sendo D e L a profundidade e a espessura da parede, respectivamente, é mostrado na Tabela 4.1. O elem
A diagonal de uma longa barra triangular se encontra isolada, enquanto as superfícies laterais, de comprimentos equivalentes, são mantidas a temperaturas uniformes Ta e Tb.Estabeleça uma rede nodal co
Uma longa barra, com seção transversal retangular, 0,4m×0,6m , e condutividade térmica igual a 1,5 W m K , está sujeita às condições de contorno mostradas na figura. Duas das laterais são mantidas a u
Lembre-se da placa retangular bidimensional do Problema 4.2. Usando um método numérico apropriado, com Δx = Δy = 0,25 m, determine a temperatura no seu ponto central (1; 0,5).