Lançamento Horizontal
Teoria
Olá galera bonita, nós somos o Responde Aí, a plataforma de exatas que vai salvar o seu semestre!!
Hoje nós vamos falar sobre o lançamento horizontal. Se você precisa aprender esse conteúdo ou está com algumas dúvidas, você chegou ao lugar certo 😉 Partiu?
Conhecimentos Prévios
Existem alguns conceitos que são bem importantes que você saiba para poder entender bem o lançamento horizontal. Eu vou deixar esses conceitos prévios listados aqui embaixo e se você ainda não entende super bem algum deles, você dá uma conferida lá e depois volta para essa página aqui, combinado?
Lançamento Horizontal
O lançamento horizontal nada mais é que o movimento de um objeto que ocorre tanto na horizontal quanto na vertical e que o objeto sai da posição inicial somente com velocidade na horizontal. O fato interessante para esse lançamento é que o movimento que ele faz na horizontal é um movimento retilíneo uniforme (MRU) enquanto o movimento na vertical é um movimento retilíneo uniformemente variado (MRUV).
Por esse motivo, para resolvermos problemas de lançamento horizontal não precisamos conhecer nenhuma fórmula nova, vamos usar as fórmulas que usamos para o MRU e para o MRUV.
Menos fórmulas para gravar!
📢 ALERTA: Acabamos de falar que para resolvermos problemas de lançamento horizontal vamos utilizar as fórmulas do MRU e MRUV, então é importante que você tenha um mente essas fórmula, beleza? Nós temos uma tabela, onde reunimos todas as fórmulas úteis de cinemática retilínea, inclusive as fórmulas que precisamos para esse conteúdo agora. Confere aqui 👇🏽
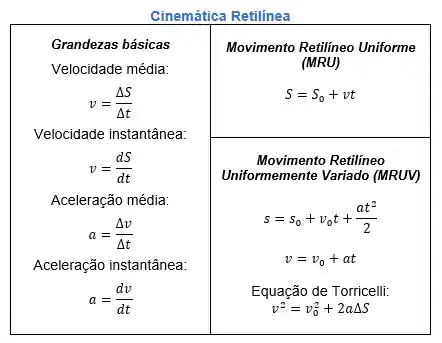
É mais fácil entender como vamos resolver um problema de lançamento horizontal através de um exemplo, então é isso que vamos fazer.
EXEMPLO: Um professor para estimular seus alunos, dá um peteleco em uma bola que está em cima de uma mesa a altura uma latura
RESOLUÇÃO:
Primeiro, em um lançamento horizontal o objeto descreve uma trajetória como mostra a figura, justamente por ter um movimento na horizontal e outro na vertical.
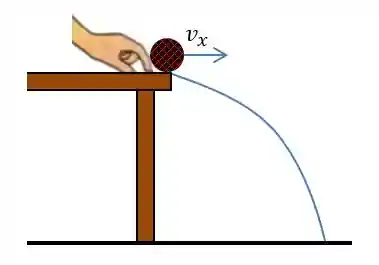
Agora, o que vamos fazer é separar os movimentos, horizontal e vertical, e resolver um eixo de cada vez. Ao separarmos esses movimentos vamos ver que o objeto terá uma velocidade no eixo
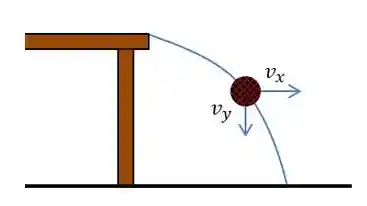
Vamos começar analisando o movimento na vertical, eixo
Dito isso, vamos utilizar a equação da posição para o movimento acelerado:
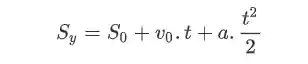
Substituindos os valores que temos conseguimos achar o tempo que a bola leva para chegar ao chão:
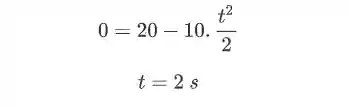
Agora, vamos analisar o movimento horizontal, eixo
Vamos usar a equação da posição para o movimento retilíneo uniforme:
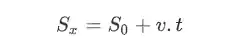
Vamos assumir que a bola parte da posição
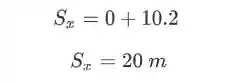
E prontinho, achamos o alcance também!
Deu pra entender como encarar um problema de lançamento vertical?
Agora que terminamos a teoria, é hora de EXERCITAR. Para isso eu vou deixar aqui embaixo 👇🏾 um vídeo, no qual um exercício é resolvido passo-a-passo com você. Dá uma conferida aí!
Exercício em vídeo
Confere esse vídeo aí de exercício resolvido passo-a-passo, tenho certeza que vai amar! 😉
Lançamento Horizontal
Exercícios Resolvidos
Exercício Resolvido #1
Seduc-PI
Num experimento, são utilizadas duas bolas de bilhar idênticas, um lançador de bolas horizontal e um ambiente com ar muito rarefeito, de maneira que os corpos em movimento apresentam resistência do ar desprezível. Por meio de sensores e fotografia estroboscópica, o experimento consiste em acompanhar o tempo de queda das duas bolas e caracterizar o tipo de movimento que elas descrevem durante a queda. As duas são colocadas numa mesma altura inicial h, ficando a bola B sobre uma plataforma. A bola A é abandonada no mesmo instante que a bola B é lançada horizontalmente com velocidade V.
Assumindo que a aceleração da gravidade é constante, é correto afirmar que:
a) a bola A tem o tempo de queda menor que o tempo de queda da bola B.
b) a bola A tem o tempo de queda maior que o tempo de queda da bola B.
c) os tempos de queda das duas bolas são iguais e a bola B descreve um movimento uniforme.
d) as duas componentes da velocidade da bola B são descritas por um movimento uniforme variado.
e) os tempos de queda das duas bolas são iguais e a bola A descreve um movimento uniforme variado.
Passo 1
O tempo de queda das bolas é determinado para o movimento vertical delas, né? Que ocorre sob ação da aceleração da gravidade, e pode ser calculado assim (considerando a velocidade sendo 0 no ponto máximo):
Como podemos ver, o tempo de queda depende apenas da altura e da gravidade de onde se encontram as bolinhas. Como elas estão na mesma altura e sujeitas a mesma aceleração da gravidade, o tempo de queda será o mesmo para as duas bolinhas, e a única diferença é que a bola B, além do movimento na vertical, executa um movimento na horizontal e para a direita.
Caindo sob a ação da força da gravidade, o movimento da bola A é retilíneo e uniformemente variado.
Resposta
e) os tempos de queda das duas bolas são iguais e a bola A descreve um movimento uniforme variado.
Exercício Resolvido #2
USP-1ª Prova-2014
Uma bola desliza sobre uma superfície horizontal sem atrito com uma velocidade até chegar a borda de uma mesa e cair em queda livre. No exato momento em que atinge o solo a velocidade da bola é . Quanto vale a componente vertical da velocidade da bola neste instante?
Passo 1
Inicialmente a bola tá deslizando sobre a mesa e ao chegar na borda a gente tem a seguinte situação:
Muito bem, a mesa não tem atrito então a bola chega à ponta da mesa com velocidade:
Ou seja a velocidade horizontal é constante!
Após isso, a bola cai da mesa e começa a sofrer ação aceleração da gravidade que vai acelerá-la na vertical e no esquema vai ficar dessa forma:
Ao chegar no solo, a bola agora terá uma componente e uma componente e o seu vetor velocidade pode ser visto como a resultante das outras duas velocidades.
E vetorialmente a gente soma as componentes dos dois vetores.
Nas alternativas o aparece em módulo, sem a indicação de vetor. Então vamos tirar o módulo de fazendo o teorema de Pitágoras com o triângulo da figura:
Daí teremos o módulo de
Pronto! Agora é só isolar o :
Enfim:
Resposta
Letra
Exercício Resolvido #3
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 1 , 8º ed. Rio de Janeiro: LTC , 2008, pp 86-25
Um dardo é arremessado horizontalmente com uma velocidade inicial de em direção a um ponto , o centro de um alvo de parede. Ele atinge um ponto do alvo, verticalmente abaixo de , s depois do arremesso. Qual é a distância ? A que distância do alvo foi arremessado o dardo?
Passo 1
O item quer saber qual a distância que o dardo anda no eixo dado que no estado inicial ele estava na posição , como queremos o deslocamento no eixo vamos usar a equação do movimento uniformemente variado para resolver este item.
Já no item ele pede a distância entre o alvo e o dardo, como se ele pedisse o alcance e por isso vamos usar a rquação do movimento uniforme para encontrar essa distância no eixo .
Passo 2
Para descobrirmos a distância , que é a posição final menos a posição inicial , vamos analisar o movimento no eixo e por isso vamos usar a equação da posição de um movimento acelerado.
O problema nos forneceu que o lançamento é horizontal, então , e ainda deu o instante que o dardo acerta o ponto , .
Como o problema pede apenas a distância entre não faz sentido colocarmos sinal na resposta, por isso
Mas vale lembrar que o sinal de negativo nos mostra que o ponto está abaixo do ponto . O que já era de se esperar por ser um lançamento horizontal.
Passo 3
A distância entre o alvo e o dardo é no eixo . Por isso vamos analisar o movimento nesse eixo para encontrarmos a resposta. Como o movimento em é uniforme temos uma única equação possível
Queremos saber o deslocamento do dado em dado que o dardo parte com velocidade de
Resposta
Exercício Resolvido #4
Hugh D. Young e Roger A. Freedman, Física I – Mecânica, 10a ed. São Paulo: Addison Wesley, 2003, pp 82 - Modificado
Uma bola de tênis rola para fora da extremidade de uma mesa situada a uma altura igual a acima do solo e atinge o solo em um ponto situado a da extremidade da mesa. Despreze a resistência do ar. Ache o tempo de percurso. Ache o módulo da velocidade inicial. Ache o módulo, a direção e o sentido da velocidade da bola imediatamente antes de a bola atingir o solo.
Passo 1
Ele diz que a bola de tênis, atinge o solo em um ponto a , essa é a maior distância horizontal que ele atinge, seu alcance.
No eixo temos um Movimento Uniforme.
No eixo , temos um lançamento vertical, que neste caso é uma queda livre.
Pelo enunciado, temos os seguintes dados:
Passo 2
O tempo de percurso é o tempo que a bola leva para chegar ao chão, então
Como não temos a velocidade inicial em e temos a velocidade inicial em , vamos usar o movimento vertical.
Passo 3
Para acharmos o módulo da velocidade inicial, devemos encontrar suas componentes. A velocidade inicial em já temos, precisamos da velocidade inicial em . Para isso vamos usar a equação da posição com o alcance.
Passo 4
Para achar o módulo da velocidade basta fazer a fórmula do módulo de um vetor.
Passo 5
A velocidade horizontal é constante, então já temos a componente horizontal da velocidade no momento que ele chega ao solo.
Devemos então encontrar a velocidade vertical que ela chega ao solo, para podermos calcular o módulo da velocidade.
Como temos um M.U.V., e encontramos o tempo no item , vamos usar a fórmula da velocidade pelo tempo.
Assim o vetor velocidade fica da seguinte forma
Passo 6
Para calcularmos o módulo vamos usar a fórmula do módulo de um vetor.
Resposta
Exercício Resolvido #5
Seduc-Pi
Um avião tipo caça, voa horizontalmente a uma altitude de 500m, com velocidade constante, cujo módulo é 360km/h, numa região em que a aceleração da gravidade tem módulo g=10m/s2 . Num determinado instante o piloto recebe uma ordem de soltar uma bomba para atingir um alvo na superfície do solo e a executa imediatamente. Desprezando os efeitos da resistência do ar e supondo a superfície do solo plana, a distância horizontal, em metros, entre o avião e o alvo, no instante em que a bomba foi abandonada, é igual a
a) 1000m
b) 1100m
c) 1200m
d) 2400m
e) 4320m
Passo 1
Primeiro vamos imaginar nossa situação, temos algo assim, ó:
Considerando que a bomba é abandonada, temos que , e como ela vai cair 500m, essa é exatamente a distância percorrida pela bombinha! Como queremos a distância horizontal da bombinha, podemos descobrir o tempo de queda da bomba (que vai ser o mesmo tempo que ela ta percorrendo uma distância na horizontal) e usarmos esse tempo pra calcular o alcance dela na horizontal, sacou? Como a bomba tá em queda, ou seja, no sentido a favor da gravidade, nossa aceleração vai ter sinal positivo. Analisando nossa equação horária do espaço de um Movimento Uniforme Variado, temos:
Como estamos tratando de um lançamento vertical, nosso espaço é a altura, e nossa aceleração é a própria gravidade, né? Então:
Como , a gente fica com:
Substituindo por 500 e g por 10, temos:
Show! Acabamos a primeira parte.
Passo 2
Agora que sabemos que o movimento da bomba durou 10 segundos e temos a sua velocidade, que é constante, ou seja, não temos aceleração na horizontal, é só usarmos aquela nossa clássica formulinha de Movimento Uniforme, da velocidade média!
Pô, temos o tempo e temos a velocidade! Agora é só jogar na formulinha! OPA! Mas peraí, né? Nossa velocidade tá em km/h, t nossas respostas estão todas em metros. Então vamos converter de km/h pra m/s, dividindo por 3,6, né? Show:
Perfeito! Agora podemos substituir:
Conseguimosss! Fechamos!
Resposta
a)1000m
Exercício Resolvido #6
Paul A. Tripler e Gene Mosca, Física Para Cientistas e Engenheiros, Volume 1, 6ª edição, Cap 3, pp 88-80
Um avião de carga está voando Horizontalmente a uma altitude de , com uma rapidez de , quando um grande caixote cai da rampa de acesso traseira. (Ignore a resistância do ar) Quanto tempo o caixote leva para chegar ao solo? Ao atingir o solo, qual é a distância horizontal do caixote ao ponto em que ele se soltou do avião? Ao atingir o solo, qual é a distância do caixote ao avião, supondo que este continuou com a mesma velocidade?
Passo 1
O problema é um lançamento horizontal, pois como o caixote estava viajando com o avião a e derrepente foi solto do avião o caixote continuará a se mover com no eixo já que o enunciado pede para desconsiderar a resistência do ar e vai começar a executar um movimento de queda livre no eixo .
Passo 2
Para descobrirmos o tempo que o caixote leva para chegar ao chão vamos olhar o movimento de queda livre no eixo . Pela equação da posição temos:
Como aceleração está em devemos passar a posição para metros também
Como o tempo sempre é positivo, podemos desconsiderar esse valor negativo que encontramos.
Passo 3
O problema nos pede o alcance do objeto, vamos analisar o movimento do caixote no eixo . Como é um lançamento horizontal sabemos que o corpo continuará se movendo com velocidade constante de no eixo .
Como a velocidade está em e o tempo em segundos, devemos passar a velocidade para
Passo 4
O avião e o caixote continuam com a mesma velocidade no eixo , por isso a distância deles no eixo é zero.
Como a avião não muda sua posição no eixo , e o caixote sai da altura e vai para zero. Temos que a distância entre els no eixo é
Vamos então representar essa distância em vetores unitários
Resposta
Exercício Resolvido #7
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 1 , 8º ed. Rio de Janeiro: LTC , 2008, pp 88-53
Uma bola rola horizontalmente do alto de uma escada com uma velocidade de . Os degraus têm de altura ede largura. Em qual degrau a bola bate primeiro?
Passo 1
A bola executa um lançamento horizontal de forma que ela vai caindo e andando para frente até encontrar o chão (um degrau qualquer da escada).
Porém o chão não é mais reto, a cada o “chão” desce . Vamos representar esse “movimento” do chão da seguinte forma , onde representa o numero de degraus. Observe que passamos o para .
Queremos descobrir para qual a equação da posição no eixo e no eixo são satisfeitas. Vamos começar analisando o movimento no eixo .
Passo 2
Vamos analisar o movimento no eixo . A bola encontrará o chão em um instante de tempo em uma posição . Como é um lançamento horizontal, sabe-se que o movimento é uniforme, sendo assim usaremos a única equação do movimento uniforme.
Considerando o início da escada sendo a posição
Podemos isolar
Passo 3
Vamos analisar o movimento no eixo agora. Como é um lançamento horizontal temos que , . Como sempre vamos chamar o chão como posição zero, e por isso temos que a bola sai da posição
Passo 4
No Passo 2 encontramos uma relação entre e , vamos substituir essa relação na equação que acabamos de encontrar para achar
No passo dois achamos que
Terminamos de achar, analisando o movimento em
Substituindo, temos
Se , teremos a posição inicial, que foi de onde a bola saiu, então esse valor de não nos interessa. Vamos achar o outro e por isso podemos cortar o
Como representa o número de degraus, isso significar que a bola baterá no chão no degraus.
Resposta
Degrau.
Exercício Resolvido #8
USP-1ª Prova-2014
Um corpo de massa sai do repouso e cai em queda livre de uma altura com relação ao solo. Quando ele passa pela altura (veja a figura abaixo) é desviado por um anteparo de modo que assume uma nova velocidade na horizontal tal que o módulo dessa velocidade é igual ao módulo da velocidade que o corpo tinha imediatamente antes de ser desviado.
Ache o vetor velocidade com que o corpo é lançado na horizontal.
A que distância de sua posição inicial o corpo atinge o solo?
Quais valores de dariam o mesmo alcance ?
Qual valor de maximiza ?
Note que para uma função , o valor que maximiza esta função é obtido tomando a derivada com relação a e igualando a zero de forma que .
Passo 1
Bem primeiramente precisamos encontrar o vetor velocidade na altura , que pelas fórmulas de movimento uniformemente variado pode ser encontrado por:
Entretanto precisamos do instante de tempo em que o corpo chega a altura , para isso vamos utilizar outra fórmula de MUV:
Substituindo os valores e lembrando que o corpo parte do repouso, portanto , encontramos:
Agora podemos isolar o tempo para encontrar o instante em que ele chega a altura :
Agora já temos o tempo para substituir na nossa fórmula:
Lembrando que no instante inicial.
Onde é o versor que indica a direção e sentido da velocidade (vertical para baixo). Ainda podemos simplificar essa expressão jogando a gravidade para dentro da raiz:
Muito bem, mas o problema quer o vetor com que o corpo é lançado na horizontal após chocar-se com o anteparo. Que segundo o enunciado possui o mesmo módulo de , logo:
Passo 2
O alcance pode ser calculado pela fórmula da posição de um movimento uniforme:
Onde o é o tempo de voo, que a gente não possui ainda. Mas a gente pode descobrir usando a seguinte fórmula para o eixo :
Onde nós sabemos que o e que , além de que pois ele inicia um novo movimento na altura onde inicial é zero. Agora vamos substituir:
Isolando o tempo , temos:
Agora podemos substituir na nossa fórmula do da posição de um movimento uniforme:
Lembrando que corresponde a velocidade inicial em que encontramos no item anterior.
Passo 3
Bem, no item anterior encontramos , note que se abrirmos essa equação ficamos com:
Logo, vemos que depende de quadraticamente, quer dizer, podem existir dois valores de para o qual essa raiz dê . Para simplificar nossa vida, vamos elevar ao quadrado os dois lados da equação, porque assim podemos sumir com essa raiz chata.
Muito bem, caímos numa equação do segundo grau, basta calcular as raízes que são:
Essas duas raízes fornecem dois valores de para o qual o alcance é .
Passo 4
Para descobrirmos o no qual o alcance é máximo, vamos seguir a dica do exercício.
Derivando a equação vamos encontrar:
Logo, para que essa divisão seja zero, o numerador precisa ser zero, portanto:
Resposta