Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 14.Exercícios e Problemas - Ex. 44

14.44. Um bloco de 5,0 kg está pendurado a uma mola com constante elástica de 2000 N/m. O bloco é puxado 5,0 cm para baixo a partir da posição de equilíbrio e lhe é comunicada uma velocidade inicial de 1,0 m/s orientada para a posição de equilíbrio. Quais são (a) a frequência, (b) a amplitude e (c) a energia mecânica total do movimento?

Passo 1

Então a gente tem a seguinte situação

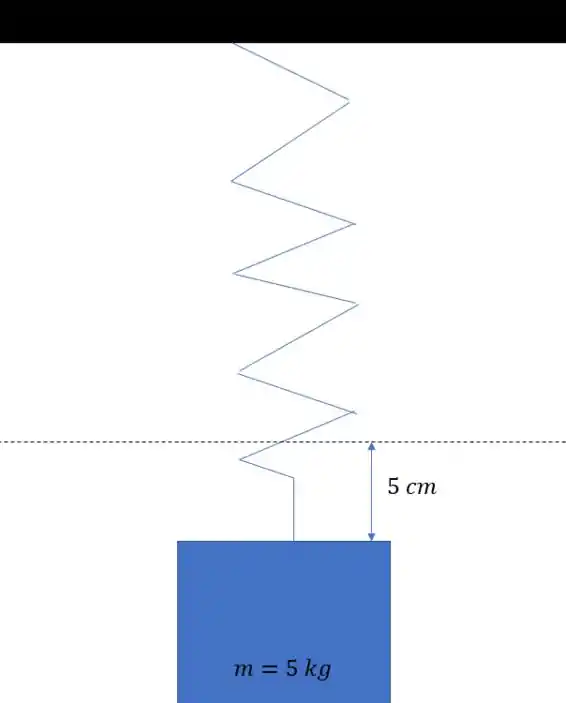
E aí o bloco começa um movimento harmônico simples.

Vamos começar pelo item (a), a frequência. A gente pode achar a frequência pela equação

f = 1 2 π k m

O enunciado nos dá a massa e a constante da mola, basta a gente substituir os valores

f = 1 2 π 2000 5 = 3,183   H z

Passo 2

Agora vamos para o item (b). A gente pode usar essa equação para descobrir a amplitude

A = x 0 2 + v 0 2 π f 2

Essa equação surge da conservação de energia.

Bom, a gente pode assumir que as condições iniciais são aquelas depois do bloco ser deslocado para baixo. Então a posição é - 0,05   m se o sentido positivo for para cima, e a velocidade é 1 m s .

Agora é só substituir os valores.

A = - 0,05 2 + 1 2 π ⋅ 3,183 2 = 0,0707   m

Passo 3

Finalmente o item (c). A energia mecânica total do movimento é a soma das energias potencial elástica e cinética. Mas a gente pode pegar um momento em que não tem energia cinética, que é na amplitude do movimento, lembre-se, no movimento harmônico, na amplitude a aceleração tem seu maior módulo e a velocidade é nula. Então

E = 1 2 k A 2

Substituindo os valores

E = 1 2 2000 0,0707 2 = 5   J

Resposta

  1. 3,183   H z
  2. 0,0707   m
  3. 5   J
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um bloco de massa M capaz de deslizar com atrito desprezível sobre um trilho por uma mola de masa desprezível e constante elástica k , inicialmente relaxada. Uma bolinha de chiclete de massa m , lança
Uma bola de massa m de massa fresca de pão cai de uma altura h sobre o prato de uma balança de mola e fica grudada nele. A constante de mola é k , e as massas da mola e do prato podem ser deprezadas.
Uma partícula de masa m está suspensa do teto por uma mola de constante elática k e comprimento relaxado l 0 , cuja massa é desprezível. A partícula é solta em repouso, com a mola relaxada. Tomando o
Use a fórmula de Euler e as regras para cálculo de produto e potências de números complexos para calcular: (a) cos ⁡ a + b e sen ⁡ a + b ; (b) cos ⁡ 3 a e sen ⁡ ( 3 a ) em função de cos ⁡ e sen ⁡ de a
64. Ao entrarem em um carro, quatro passageiros com massa total igual a 250k g comprimem em 4,0c m as molas de um carro com amortecedores gastos. Considere o carro e os passageiros como um único corpo