Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Moysés - Vol. 2 - Ed: 4º - Capítulo 3.Problemas - Ex. 5

Uma bola de massa m de massa fresca de pão cai de uma altura h sobre o prato de uma balança de mola e fica grudada nele. A constante de mola é k , e as massas da mola e do prato podem ser deprezadas. (a) Qual é a amplitude de oscilação do prato? (b) Qual é a energia total de oscilação?

Passo 1

(a) Quando cair sobre a mola, a massa vai entrar em movimento harmônico simples. Podemos descrever esse movimento pela seguinte equação geral:

x t = A cos ⁡ ω t + ϕ

Onde ω 2 = k / m . Para encontrar o valor de A , precisamos procurar as condições iniciais.

Vamos definir que x = 0 está no ponto de equilíbrio. Esse é o ponto em que o peso da massa está equilibrado com a força elástica da mola:

k Δ x = m g

Δ x = m g k

Isso quer dizer que a mola tem que ser distorcida por m g / k para entrar em equilíbrio:

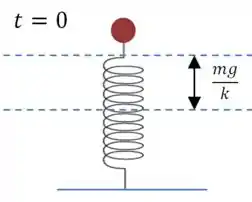
Então a posição inicial da massa é:

x 0 = m g k

Essa é nossa primeira condição inicial.

Passo 2

Para encontrar a velocidade inicial só precisamos usar a conservação de energia.

A massa cai por uma altura h até atingir a mola. Isso quer dizer que ela converte energia potencial gravitacional em energia cinética:

m g h = 1 2 m v 2

v = 2 g h

Então nossa segunda condição inicial é:

v 0 = x ˙ 0 = 2 g h

Passo 3

Agora é só aplicar essas duas condições inicias para encontrar A :

x 0 = m g k x ˙ 0 = 2 g h

Começando pela primeira:

x t = A cos ⁡ ω t + ϕ

x 0 = A cos ⁡ ϕ = m g k

E para aplicar a segunda temos que derivar a função x t :

x ˙ t = - A ω sen ⁡ ω t + ϕ

x ˙ 0 = - A ω sen ⁡ ( ϕ ) = 2 g h

Então:

- A ω sen ⁡ ( ϕ ) = 2 g h A cos ⁡ ( ϕ ) = m g k

Vamos isolar o seno e o cosseno, e elevar tudo ao quadrado:

sen 2 ⁡ ϕ = 2 g h A ω 2 cos 2 ⁡ ϕ = m g k A 2

Agora podemos somar as duas equações:

sen 2 ⁡ ϕ + cos 2 ⁡ ϕ = 2 g h A ω 2 + m g k A 2 = 1

Então:

A 2 = 2 g h ω 2 + m 2 g 2 k 2

Lembrando que ω 2 = k / m :

A 2 = 2 g h m k + m 2 g 2 k 2

A 2 = m g k 2 1 + 2 k h m g

A = m g k 1 + 2 k h m g

Passo 4

(b) Agora vamos lembrar da fórmula para a energia total de um oscilador harmônico:

E T = k A 2 2

E T = k 2 m g k 1 + 2 k h m g 2

E T = m g 2 2 k 1 + 2 k h m g

E T = m g 2 2 k + m g h

Resposta

(a) A amplitude de oscilação é A = m g k 1 + 2 k h m g .

(b) A energia total é E T = m g 2 2 k + m g h .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um sistema oscilatório massa-mola oscilante leva 0,75s para começar a repetir seu movimento. Determine (a) o período, (b) a frequência em hertz e (c) a frequência angular em radianos por segundo.
Do ponto de vista das oscilações verticais, um automóvel pode ser considerado como estando apoiado em quatro molas iguais. As molas de um carro são ajustadas de tal forma que as oscilações têm uma fre
Um corpo de 0,12k g executa um movimento harmônico simples de amplitude 8,5c m e período 0,20s . (a) Qual é o módulo da força máxima que age sobre o corpo? (b) Se as oscilações são produzidas por uma
Um oscilador é formado por um bloco com uma massa de 0,500k g ligado a uma mola. Quando é posto em oscilação com uma amplitude de 35,0c m , o oscilador repete o movimento a cada 0,500s . Determine (a)
13.10P Quando forçado pela mola, a roda vista na Figura 13.16 rola sobre o piso, girando em torno de seu eixo. Calcule a frequência de oscilação do sistema.