Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 14.Questões Conceituais - Ex. 4

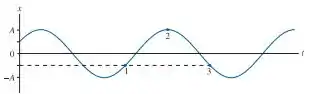
A FIGURA Q14.4 mostra um gráfico posição versus tempo para uma partícula em MHS.

a. Qual é a constante de fase ϕ 0 ? Explique.

b. Qual é a fase da partícula em cada um dos três pontos numerados no gráfico?

Passo 1

Olhando para o gráfico, vemos que a amplitude da partícula é A . Ora, sabemos que para um MHS, podemos equacionar x em função de t da seguinte maneira:

x = A cos ⁡ ω t + ϕ 0

onde ω é a frequência angular e ϕ 0 é a fase inicial, obtida quando t = 0 .

Passo 2

  1. Inicialmente, observamos que para t = 0 , temos x = A / 2 . Assim,

    2. x = A cos ⁡ ω t + ϕ 0 A 2 = A cos ⁡ ω ⋅ 0 + ϕ 0 cos ⁡ ϕ 0 = 1 2

    Assim, temos duas possibilidades para ϕ 0 !

    1. ϕ 0 = π / 3 ;
    2. ϕ 0 = 5 π / 3 .

    Qual valor devemos escolher? Devemos analisar a velocidade! Note que em t = 0 a velocidade é positiva, pois estamos indo para valores cada vez maiores de x . Como:

    v t = - A ω sin ⁡ ω t + ϕ 0 v 0 = - A ω sin ⁡ ϕ 0

    segue que v > 0 quando sin ⁡ ϕ 0 < 0 (por causa do sinal de menos na expressão de v ). Como

    1. sin ⁡ π 3 = 3 / 2
    2. sin ⁡ 5 π 3 = - 3 / 2

    segue que ϕ 0 = 5 π / 3 .

    Passo 3

  2. A fase ϕ é definida como

ϕ = ω t + ϕ 0

Assim, temos

x = A cos ⁡ ϕ

  1. Quando estamos no ponto 1 , x = - A / 2 e a velocidade é positiva. Assim,

    2. - A 2 = A cos ⁡ ϕ cos ⁡ ϕ = - 1 2 ϕ = 2 π / 3 o u 4 π / 3

    Como a velocidade é positiva, devemos escolher ϕ tal que sin ⁡ ϕ < 0 (por causa do mesmo argumento usado no item a.). Como

    1. a sin ⁡ 2 π 3 = 3 2
    2. sin ⁡ 4 π 3 = - 3 2

    segue que ϕ 1 = 4 π / 3 .

  2. Quando estamos no ponto 2 , x = A . Assim,

    3. A = A cos ⁡ ϕ cos ⁡ ϕ = 1 ϕ = 0

    Segue que ϕ 2 = 0 .

  3. Quando estamos no ponto 3 , temos x = - A e a velocidade negativa.

Aqui, estamos na mesma situação do ponto 1, porém apenas a velocidade trocou de sinal. Portanto, temos ϕ = 2 π / 3 .

Resposta

  1. 5 π / 3 .
  2. ϕ 1 = 4 π / 3 ϕ 2 = 0 ϕ 3 = 2 π / 3  
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

17. Sobre um trilho de ar sem atrito, horizontal, um corpo oscila na extremidade de uma mola ideal de constante 2,50N / c m . O gráfico da Figura 13.31 mostra a aceleração do corpo em função do tempo.
Ache o movimento resultante de dois movimentos harmônicos simples na mesma direção dados por: x 1 = cos ⁡ ω t - π 6 , x 2 = sen ⁡ ω t . Represente graficamente os respectivos vetores girantes.
Trace as figuras de Lissajous corerespondentes à composição dos seguintes movimentos harmônicos simples em direções perpendiculares:(a) x = A cos ⁡ ω t , y = A sen ⁡ 2 ω t .(b) x = A sen ⁡ ω t , y = A
A FIGURA P14.32 é o gráfico velocidade versus tempo de uma partícula em movimento harmônico simples. a. Qual é a amplitude da oscilação? b. Qual é a constante de fase? c. Qual é a posição para t =0s ?
A FIGURA P14.31 é o gráfico posição versus tempo de uma partícula em movimento harmônico simples. a. Qual é a constante de fase? b. Qual é a velocidade em t =0s ? c. Quanto vale v m á x á ?