68. Em sua primeira viagem ao Planeta , você leva consigo uma massa de , uma mola de 40 cm de comprimento, uma régua e um cronômetro. Você está curioso para saber qual é a aceleração de queda livre no Planeta , onde as tarefas comuns parecem mais fáceis de realizar do que na Terra, todavia não consegue encontrar essa informação no Guia do Visitante. Certa noite, você suspende a mola no teto de seu quarto e prende a massa a ela. Então, descobre que, com isso, a massa estica a mola em . Depois, você puxa a massa para baixo e a solta. Com o cronômetro, você constata que oscilações duram . E agora, você pode satisfazer à sua curiosidade?
Passo 1
Opa! E aí brother! Aqui vamos nós de novo!
Se liga só! A primeira coisa que devemos fazer, é um esboço pra representar melhor o que está acontecendo, inclusive posicionando um referencial pra ficar do jeito mais claro possível.
E aqui está nossa bela figura...
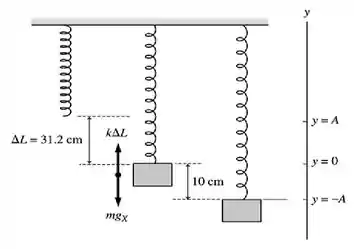
Passo 2
Aí já sabe o que tem que fazer, né companheiro!?
Partiu usar a segunda lei de Newton pro eixo :
Temos duas forças em nosso sistema, a força restauradora da mola e a força peso, apontando para baixo...
Como para o movimento harmônico simples...
Logo, a nossa relação anterior pode ser reescrita como...
Isolando e considerando o fato de que a frequência angular é a mesma coisa que;
Ficamos com... Lembrando que esse é o período de oscilações, hein!?
E pronto! Essa é gravidade do Planeta !