Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 14.Exercícios e Problemas - Ex. 76
76. Um bloco de está preso a uma mola horizontal com constante elástica de . Ele se encontra em repouso sobre uma superfície horizontal desprovida de atrito. Um projétil de é disparado contra o bloco, na direção oposta à da mola, e se incrusta no bloco.
a. Qual era o valor da velocidade do projétil se as oscilações subsequentes têm amplitude de ?
b. Você poderia determinar a velocidade do projétil medindo a frequência de oscilação? Em caso afirmativo, como o faria? Se não for possível, explique por quê.
Passo 1
Opa! Hey brother! Bora pra mais uma questãozinha sobre Ondulatória!
Se liga só! Pra resolver essa questão, primeiramente bora fazer um esboço para o nosso bloco quando ele está executando suas oscilações.
E aqui está...
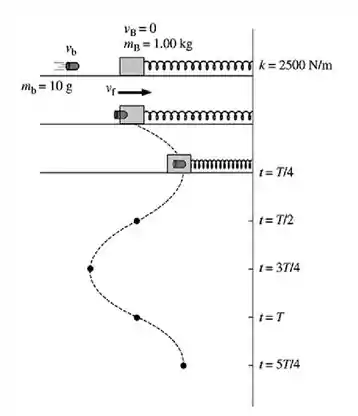
Passo 2
a) A questão nos diz que a bala, ficou incrustada no bloco... Ora bolas! Isso é sinal de que temos uma colisão inelástica por aí. E em colisões inelástica, já sabe né!? A energia não é perdida pela colisão!
Desse modo, aplicando a conservação da energia mecânica, relacionando os momentos no qual o bloco é atingido pela bala na posição de equilíbrio e o momento no qual o bloco está em amplitude máxima...
Na posição de equilíbrio, a velocidade do bloco é máxima... Isto ocorre logo após o impacto da bala e não há energia potencial presente.
Já na máxima amplitude, o único tipo de energia presente é a potencial elástica. Sendo assim;
Lembrando que a massa da bala também vai aparecer na expressão, hein!?
Isolando , que é a velocidade máxima do bloco no equilíbrio, então...
Essa é a velocidade do sistema bala-bola após o impacto do projétil!
Passo 3
Em seguida, como temos uma colisão, apliquemos a conservação do momento antes e depois do impacto da bala no bloco...
Como o bloco estava em repouso antes da colisão, então...
E substituindo os valores numéricos de cada variável...
Obtemos finalmente o valor da velocidade do projétil antes da colisão!
Passo 4
b) Quanto a essa letra! Bom! Tá na cara a resposta...
Presta bem atenção! A frequência angular do nosso sistema depois da colisão da bala com o bloco, obviamente é dada por...
Ou seja, por essa fórmula vemos que não há nenhuma relação entre a velocidade e a frequência angular.
A frequência angular está relacionada apenas com a massa e a constante elástica da mola!
De modo que a nossa resposta é um sonoro
Pronto! Terminamos aqui!
Até a próxima!
Resposta
a)
b)