Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 14.Exercícios e Problemas - Ex. 33
Os dois gráficos da FIGURA P14.33 representam dois diferentes sistemas massa-mola verticais.
a. Qual é a frequência do sistema A? Qual é o primeiro instante de tempo em que a massa apresenta velocidade máxima quando está se deslocando verticalmente para cima?
b. Qual é o período do sistema B? Qual é o primeiro instante de tempo em que a energia é inteiramente do tipo potencial?
c. Se os dois sistemas possuem a mesma massa, quanto vale a razão entre suas constantes elásticas?
Passo 1
Em o sistema oscila 3 vezes (tem três picos além do primeiro), então o período do sistema é de:
Então sua frequência será de:
E a velocidade máxima é sempre atingida quando a posição está em , e dividindo a linha do tempo direitinho vemos que:
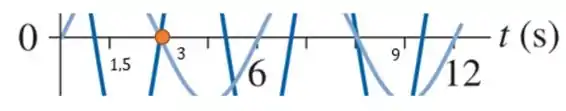
A primeira vez que a onda atravessa o eixo e está subindo (que é o interesse da questão, pois note que ela até atravessa o eixo porém ele está descendo) é em .
Uma vez que quando a energia potência se anula (que só ocorre em , ou a deformação da mola sendo nula) temos a energia cinética sendo a energia mecânica do sistema (e esse é o valor máximo para a energia cinética)
Passo 2
Já para o sistema temos duas oscilações em , então o período de uma oscilação se dará em .
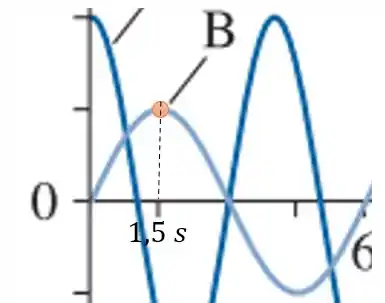
E assim como temos a máxima velocidade quando o sistema cruza o eixo , nós temos que os picos e os vales dessa função periódica são os momentos quando a energia potencial é máxima. Lembre-se da fórmula da energia potencial elástica, pois como vimos o sistema massa mola quando temos a massa na posição de amplitude a velocidade zera e a energia potencial chega no seu maior valor.
E pelo gráfico vemos que seu primeiro pico é em .
Passo 3
O período do sistema pode ser calculado como:
E no sistema :
Como então , com sendo uma constante, logo:
Igualando nos dois lados:
E isso pode ser escrito como:
Arrumando pro que queremos para a letra :
Porém dos passos anteriores vimos que e , então: