Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 14.Exercícios e Problemas - Ex. 46

Um bloco de 200 kg está pendurado a uma mola com constante elástica de 10 N/m. Em t = 0 s, o bloco encontra-se 20 cm abaixo da posição de equilíbrio, deslocando-se para cima a uma velocidade de 100 cm/s.

a. Qual é a frequência de oscilação do bloco?

b. Qual é a sua distância do equilíbrio quando a velocidade é de 50 cm/s?

c. Qual é sua posição para t = 1,0 s?

Passo 1

Observação: o valor correto para massa é 200   g (e não kg!).

A figura abaixo representa a situação dada no enunciado.

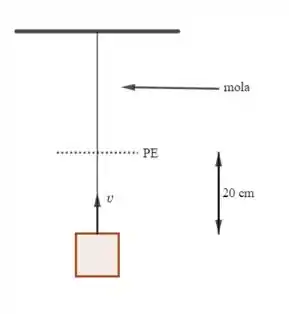
O ponto de equilíbrio é quando o bloco passa pela região onde a aceleração é nula; ou seja, ocorre quando F e l á s t i c a = m g .

Passo 2

  1. A frequência de oscilação é a mesma para o caso do MHS horizontal (que já estamos acostumados):

    2. f = 1 2 π k m f = 1 2 π 10 0,2 f = 1,13   H z

    Passo 3

  2. Podemos conservar a energia:

    3. 1 2 m v 1 2 + 1 2 k x 1 2 = 1 2 m v 2 2 + 1 2 k x 2 2

    onde v é a velocidade e x é a distância até a posição de equilíbrio. Assim, para o instante inicial, temos v 1 = 1   m / s e x 1 = 0,2   m ; para o instante final, temos v 2 = 0,5   m / s e queremos descobrir x 2 :

    1 2 0 , 2 1 2 + 1 2 10 0,2 2 = 1 2 0 , 2 0,5 2 + 1 2 10 x 2 2 x 2 = 0,23   m = 23   c m

    Aprofundamento: você pode ter se perguntado: eu não devia colocar a energia potencial gravitacional na equação da conservação da energia?? Note que 1 2 k x 2 na equação acima, na verdade não representa a energia potencial elástica, mas sim uma combinação da energia potencial elástica com a energia potencial gravitacional. Explicarei melhor:

    Note que x é a distância entre o PE (ponto de equilíbrio) até a posição da caixa. Porém, o PE estará a uma distância d abaixo de onde a mola possui comprimento natural (veja a figura)

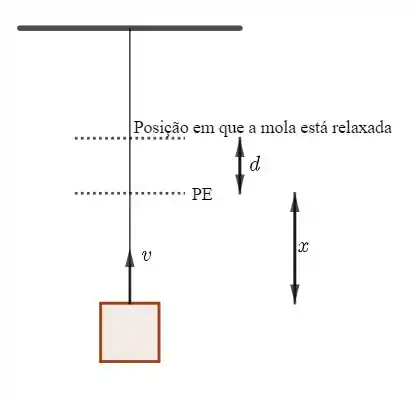
    Essa distância d pode ser obtida através de:

    m g = k d Suponha que P E seja a posição de energia potencial gravitacional nula. Logo, quando a caixa está a uma distância x do PE, temos:

    U = U e l á s t i c a + U g r a v i t a c i o n a l U = 1 2 k x + d 2 + m g - x U = 1 2 k x 2 + 2 x d + d 2 - m g x U = 1 2 k x 2 + k x d + 1 2 k d 2 - m g x U = 1 2 k x 2 + 1 2 k d 2 + x k d - m g

    Porém, já vimos que m g = k d ∴ k d - m g = 0 . Logo,

    U = 1 2 k x 2 + 1 2 k d 2

    Porém, esse 1 2 k d 2 é uma constante. Lembre-se que se adicionarmos uma constante a uma energia potencial nada é alterado! Assim, podemos dizer que a energia potencial efetiva durante o movimento da caixa é dada simplesmente por:

    U = 1 2 k x 2

    onde x é a distância da caixa até o PE!!!

    Passo 4

  3. Sendo x a posição da caixa em relação ao ponto de equilíbrio (PE), temos:

x t = x 0 cos ⁡ ω t + ϕ 0

onde x 0 é a amplitude. Podemos calcular x 0 da seguinte maneira: quando a caixa pela posição x = x 0 , v = 0 . Assim, conservando a energia:

1 2 m v 1 2 + 1 2 k x 1 2 = 1 2 k x 0 2 1 2 0,2 1 2 + 1 2 10 0,2 2 = 1 2 10 x 0 2 x 0 = 0,245   m

Para calcularmos ω , temos:

ω = 2 π f ω = 2 π 1,13 = 7,071   r a d / s

Logo,

x = 0,245 cos ⁡ 7,07 t + ϕ 0

Quando t = 0 , temos x = - 0,2   m . Logo,

x 0 = x 0 cos ⁡ ϕ 0 - 0,2 = 0,245 cos ⁡ ϕ 0 cos ⁡ ϕ 0 = - 0,816 ⟹ ϕ 0 = ± 2,526   r a d

Qual valor de ϕ 0 devemos escolher?? Para determinarmos isso, vamos ver como se comporta a velocidade.

A velocidade será dada por:

v t = d d t x t v t = - x 0 ω sin ⁡ ω t + ϕ 0 v 0 = - x 0 ω sin ⁡ ϕ 0

A velocidade inicial é positiva (pois está para cima). Logo, devemos ter sin ⁡ ϕ 0 < 0 . Portanto, devemos escolher ϕ 0 = - 2,526   r a d !!

∴ x = 0,245 cos ⁡ 7,071 t - 2,526

Fazendo t = 1,0   s :

x = 0,245 cos ⁡ 7,071 ⋅ 1 - 2,526 x = - 0,0408   m x = - 4,09   c m

Resposta

  1. 1,13   H z .
  2. 23   c m .
  3. - 4,09   c m .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

74. Um fio de 1,80m de comprimento é suspenso verticalmente. Quando uma bola de aço de 60,0k g é suspensa na extremidade do fio, este se dilata 2,0m . Se a bola for puxada para baixo a uma distância a
67. Um prato uniforme, horizontal, de 1,50k g é preso a uma mola vertical ideal de constante igual a 185N / m , e uma esfera de metal de 275g está sobre o prato. A mola está sob o prato, podendo oscil
96. Duas molas, cada uma com um comprimento sem deformação igual a 0,200m , porém com constantes diferentes de equilíbrio, k 1 e k 2 , são ligadas as extremidades opostas de um bloco de massa m apoiad
99. Mola com massa. Em todos os problemas anteriores desse capítulo consideramos molas com massas desprezíveis. Porém, é claro que toda mola possui alguma massa. Para estudar o efeito da massa da mola
14.41. Um bloco preso a uma mola é puxado para a direita e liberado em t=0 s. Ele passa por x=3,00 cm em t=0,685 s por x=-3,00cm em t=0,886 s.a. Qual é a frequência angular?b. Qual é a amplitude