Enunciado
Física - Moysés - Vol. 2 - Ed: 4º - Capítulo 4.Problemas - Ex. 9
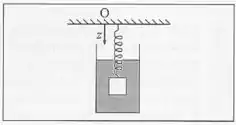
Um bloco cúbico de de aresta e densidade está suspenso do teto por uma mola de constante elástica e comprimento relaxado de , e mergulhado dentro de um fluido viscoso de densidade . Na situação considerada, a resistência do fluido é proporcional à velocidade, com coeficiente de proporcionalidade . Inicialmente em equilíbrio, o bloco é deslocado de para baixo e solto a partir do repouso. Com origem no teto e eixo vertical orientado para baixo, determine a coordenada da extremidade superior do bloco em função do tempo.
Passo 1
Temos um total de quatro forças atuando sobre o bloco: a força de atrito com um fluido, a força elástica da mola, o empuxo exercido pelo fluido e o peso do bloco.
Vamos escrever expressões para cada uma dessas forças. A coordenada dá a altura do bloco em relação ao teto:
Onde é a viscosidade do fluido.
Onde é o comprimento inicial da mola.
Onde é a densidade do fluido e é comprimento da sua aresta.
Onde é a densidade do bloco. Substituindo tudo na segunda lei de Newton, temos o seguinte resultado:
Dividindo tudo por e reorganizando um pouco, ficamos com o seguinte resultado:
A partir dessa equação, nós podemos definir a frequência natural:
E o fator de amortecimento é:
Passo 2
Beleza, voltando para a nossa equação:
Vamos começar encontrando a solução da equação homogênea, ou seja:
Com os valores que encontramos para e , no último passo, podemos ver que:
Ou seja, o movimento é subamortecido. E a solução geral é:
E podemos definir a frequência usando uma fórmula:
Então nossa solução homogênea é:
Passo 3
Agora vamos procurar a solução particular:
Todos os termos do lado direito são constantes então vamos chutar uma solução constante:
Substituindo na EDO, ficamos com o seguinte:
Substituindo os valores numéricos:
Então a solução geral é:
Agora falta impor as condições iniciais para encontrar as constantes e .
Passo 4
O bloco é deslocado de a partir do equilíbrio.
Já que encontramos uma solução particular constante , podemos garantir que ela corresponde à situação de equilíbrio do sistema, então:
Vamos aplicar essa condição sobre a nossa solução geral:
A segunda condição inicial nos diz que o bloco parte do repouso, então:
Vamos encontrar (lembre de aplicar a regra do produto):
Então:
Resposta
A coordenada é dada por .