Um fio de arame de comprimento é dobrado ao meio, formando um ângulo de , e é suspenso pelo vértice , oscilando num plano vertical. Calcule o período de pequenas oscilações em torno da posição de equilíbrio.
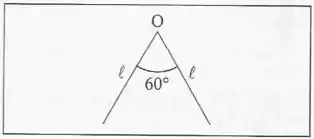
Passo 1
Vamos começar determinando o momento de inércia do sistema em relação ao ponto . Podemos tratar cada pedaço do arame como uma barra homogênea:
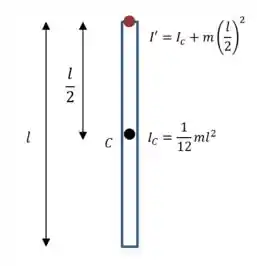
Nós conhecemos o momento de inércia em relação a um eixo que passa pelo centro:
E podemos usar o teorema dos eixos paralelos para encontrar o momento em relação a um eixo que passa pela extremidade:
E como temos dois arames, o momento de inércia total do sistema é:
Passo 2
Agora vamos pensar nas forças que agem sobre o sistema:
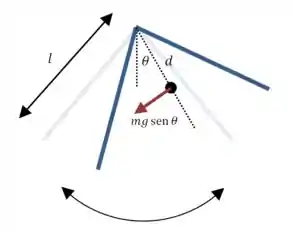
Vamos aproximar e substituir a expressão para o momento de inércia:
Ainda falta encontrar a posição do centro de massa.
Passo 3
Os dois arames têm o mesmo comprimento, e estão separados por um ângulo de . Ou seja, eles formam um triângulo equilátero.
Vamos lembrar da fórmula para a altura desse triângulo:
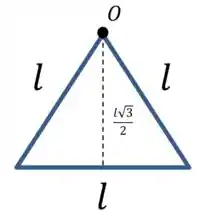
E o centro de massa está na metade da altura desse triângulo, então sua distância até o ponto é:
Vamos substituir isso na equação lá de cima:
Que é a equação de um oscilador com a seguinte frequência angular:
E o seguinte período:
Resposta
O período de pequenas oscilações em torno do equilíbrio é .