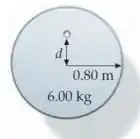
A figura mostra um disco uniforme que tem um raio , uma massa de , e um pequno buraco a uma distância do centro de disco que pode servir como ponto de suspensão. (a) Qual deve ser a distância para que o período desse pêndulo físico seja ? (b) Qual deve ser a distância para que este pêndulo físico tenha o menor período possível? Quanto vale este menor período possível?

(a) Agora vamos substituir isso na fórmula, e calcular o valor de para o qual :

Vamos dividir por no numerador e no denominador da fração, e elevar os dois lados ao quadrado:

Agora vamos transformar isso em uma equação do segundo grau para :

E podemos substituir os valores numéricos para resolver a equação:

Então:

E as duas soluções são:

A solução é maior que o raio do disco, então não faz sentido para nós nesse caso, portanto:

(b) Agora vamos encontrar o valor de que minimiza o período. Em outras palavras, queremos o valor de que satisfaz essa equação:

Lembrando que a equação para o período em função de era:

A derivada em relação a é (temos que usar a regra da cadeia e a regra do quociente):

Quando igualamos isso a zero (sabendo que ), essa expressão fica bem mais simples:

Agora vamos calcular o período nesse ponto de mínimo. Temos que substituir na nossa fórmula:

E agora substituímos os valores numéricos: